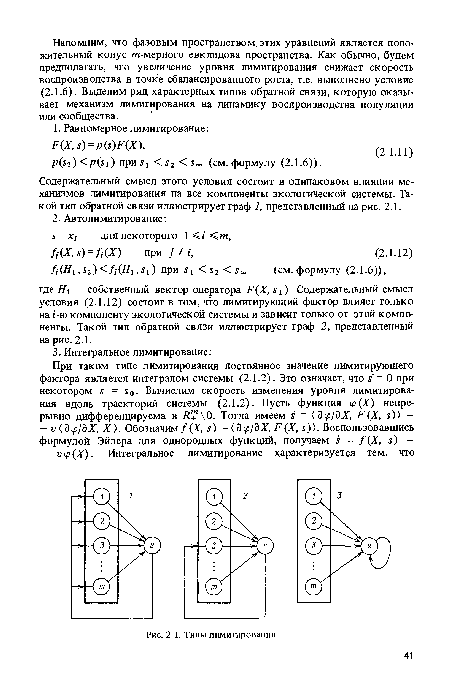
Содержательный смысл этого условия состоит в одинаковом влиянии механизмов лимитирования на все компоненты экологической системы. Такой тип обратной связи иллюстрирует граф 1, представленный на рис. 2.1.[ ...]
Содержательный смысл условия (2.1.13) состоит в том, что система стремится ’’стабилизировать” некоторое стационарное значение лимитирующего фактора. Соответствующий случаю (2.1.13) тип обратной связи иллюстрирует граф 3, представленный на рис. 2.1.[ ...]
Перечисленные механизмы лимитирования гарантируют стремление к равновесному состоянию в модели динамики численности популяций и сообществ при отсутствии внешних источников.[ ...]
Теорема 2.1.5. Пусть уравнение (2.1.2) имеет ненулевое стационарное решение Х0, s0 = ф(Х0) (so < s«,). Если выполнено условие (2.1.11), (2.1.12) или (2.1.13), то всякое решение уравнения (2.1.2),начинающееся в 0, стремится к стационарной точке Х0 при t -+°°.[ ...]
Действительно, Г (т)Я > Я при достаточно малом г, так как Х х=Н > О- Рас суждая по индукции и пользуясь монотонностью имеем г”(т)Я = Г (пт)Н- > 5» Т(кт)Н > Я при любых п > к > 1.[ ...]
Предложение 2.1.4. Если оператор Р (X, х) непрерывно дифференцируем по ЯГ в точке X = 0, то имеет место представление F(ЯГ, х) = А (я)X, где А (х) при каждом фиксированном х является матрицей с неотрицательными недиагональными элементами.[ ...]
Теорема 2.1.6. Если функции Р (X, з) и <р (X) непрерывно дифференцируемы в окрестности стационарной точки Х0, х0 = <р(Х) уравнения (2.1.2) и выполнены условия теоремы 2.1.5, то стационарное решение асимптотически устойчиво по Ляпунову в Я£ 0.[ ...]
Доказательство. Вначале докажем следующий технический результат. Лемма 2.1.6.1. Если оператор Р X) квазимонотонен, положительно однороден и неразложим, то его собственный вектор Я, отвечающий собственному значению X, является собственным вектором неразложимой матрицы с неотрицательными недиагональными элементами Ш) и X - собственное значение этой матрицы с максимальной вещественной частью.[ ...]
Перейдем к доказательству теоремы. В силу теоремы 2.1.5 достаточно ограничиться констатацией устойчивости ”в малом”.[ ...]
Рисунки к данной главе:
| Типы лимитирования |
 |
Аналогичные главы в дргуих документах:
| См. далее:Устойчивость стационарных решений |