В § 2, 3 этой главы мы провели предварительный анализ феномена диффузионной неустойчивости в системе из двух видов. Здесь же мы продолжим этот анализ, но более строго.[ ...]
Если одно из этих неравенств нарушается при некотором значении параметра д = д , то мы будем говорить, что имеет место потеря устойчивости стационарного однородного решения Л/’ (д). Если для некоторого значения М = М второе неравенство обращается в равенство (сЫ/, м = 0), то при этом в спектре оператора Я появляется одно нулевое собственное значение, а если же в равенство обращается первое неравенство (ерЬм = 0), то в спектре Я появляются два комплексно-сопряженных собственных значения. В первом случае почти всегда возникает стационарное неоднородное по пространству решение (диссипативная структура), а во втором — периодическое во времени решение. Поэтому первый вариант потери устойчивости стационарного однородного решения будем называть стационарной потерей устойчивости, а второй — колебательной потерей устойчивости.[ ...]
Очевидно, что границы областей устойчивости будут задаваться равенствами ьрЬм = 0 и сЫ Ьм = 0. Для более наглядного представления этих границ выберем один из трех параметров (£, а 1 или а г) при фиксированных 5 и двух других параметрах (например, а 1 и а%, если выбран параметр g ). Тогда в плоскости выбранного параметра и М (например, в плоскости g, М ) можно исследовать границу устойчивости.[ ...]
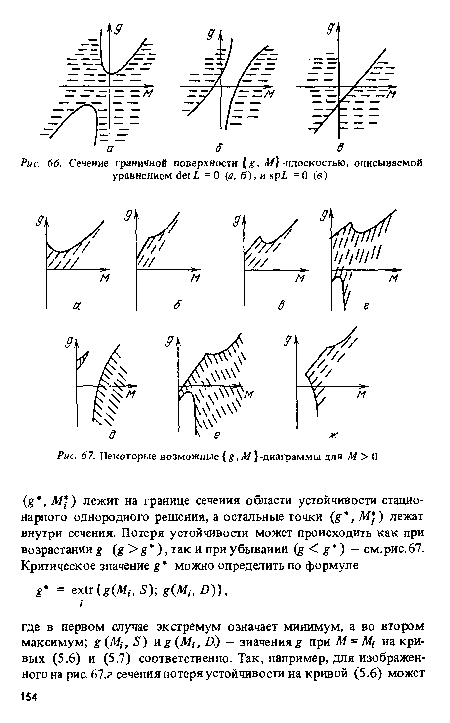
Различные типы (g,M) — диаграмм изображены на рис. 67 (для случая М> 0).[ ...]
Аналогичные диаграммы будут и для случая М < 0, но только из-за указанных выше особенностей, связанных с выполнением условия sp Ьм < 0, ограничения сверху переходят в ограничения снизу. Представление области устойчивости в виде (g, М) — диаграмм позволяет наглядно исследовать характер потери устойчивости при вариациях параметров g и М. Заметим, что последний полностью определяется геометрией области и типом граничных условий.[ ...]
Более внимательное рассмотрение рис. 67 демонстрирует нам, что геометрия областей устойчивости может быть весьма причудливой. Возникает естественный вопрос: а возможна ли разумная классификация этих областей (или их сечений) ? Оказывается, возможна, и для этого достаточно на оси М распределить, проранжировав, М-координаты характерных точек (центра гиперболы, их экстремумов — если они существуют, точек пересечения прямой и ветвей гиперболы) и Л/-координаты точек, в которых значение g на прямой (5.7) совпадает с значением g в экстремуме гиперболы. Каждому такому набору соответствует определенное сечение области устойчивости плоскостью g, М), а каждому такому сечению отвечает определенный набор возможных типов потери устойчивости при изменении g. Для того чтобы сделать эту классификацию конструктивной, можно, например, зафиксировать 6, а плоскость оставшихся параметров (вь д2) разбить на области, соответствующие определенным типам Сечений.[ ...]
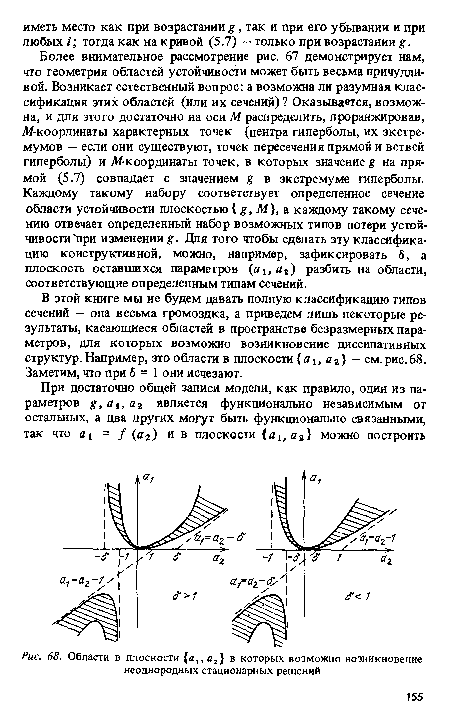
В этой книге мы не будем давать полную классификацию типов сечений - она весьма громоздка, а приведем лишь некоторые результаты, касающиеся областей в пространстве безразмерных параметров, для которых возможно возникновение диссипативных структур. Например, это области в плоскости а ь а2 - см. рис.68. Заметим, что при 6 = 1 они исчезают.[ ...]
Рисунки к данной главе:
| Некоторые возможные {£,.Л/}-диаграммы для М> 0 |
 |
| Области в плоскости {а,, а,} в которых возможно возникновение неоднородных стационарных решений |
 |