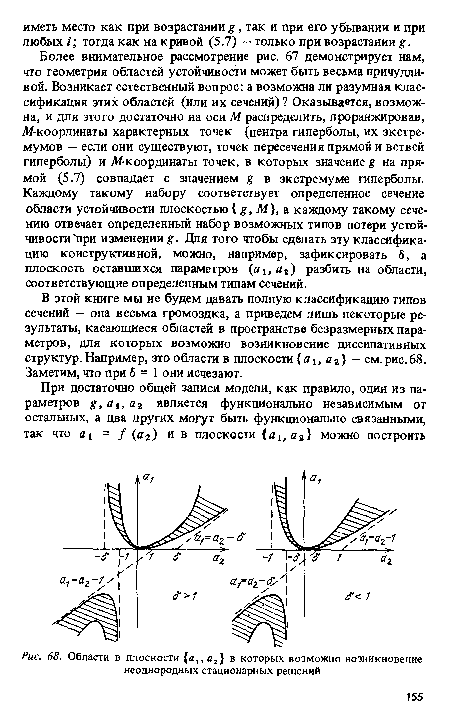
Более внимательное рассмотрение рис. 67 демонстрирует нам, что геометрия областей устойчивости может быть весьма причудливой. Возникает естественный вопрос: а возможна ли разумная классификация этих областей (или их сечений) ? Оказывается, возможна, и для этого достаточно на оси М распределить, проранжировав, М-координаты характерных точек (центра гиперболы, их экстремумов — если они существуют, точек пересечения прямой и ветвей гиперболы) и Л/-координаты точек, в которых значение g на прямой (5.7) совпадает с значением g в экстремуме гиперболы. Каждому такому набору соответствует определенное сечение области устойчивости плоскостью g, М), а каждому такому сечению отвечает определенный набор возможных типов потери устойчивости при изменении g. Для того чтобы сделать эту классификацию конструктивной, можно, например, зафиксировать 6, а плоскость оставшихся параметров (вь д2) разбить на области, соответствующие определенным типам Сечений.
Скачать страницу
[Выходные данные]