Экология СПРАВОЧНИК

Поскольку различия решении для w и р , взятых при г = ц и г == 0, также малы, то уравнения (5.2.10) и (5.2.11) можно записывать при г = 0, что справедливо с точностью используемой аппроксимации первого порядка.[ ...]

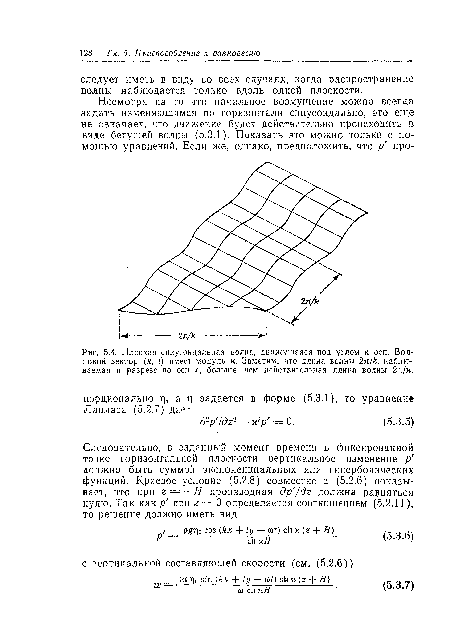
Задача свелась к решению уравнения Лапласа (5.2.7) при граничных условиях (5.2.8) на дне и (5.2.10), (5.2.11) при Z — 0. Фактически она имеет множество решении, зависящих от начального условия, т. е. от характера возмущения в начальный момент. В следующем разделе будут рассмотрены решения, в которых рг синусоидально меняется по горизонтали. Это не приводит к существенным ограничениям, поскольку, согласно теореме Фурье, произвольное возмущение можно представить в виде суперпозиции таких волн.[ ...]

Это важное уравнение определяет частоту и, следовательно, фазовую скорость волн с заданным волновым числом. Называют его дисперсионным соотношением. Приведенное выше дисперсионное соотношение было получено Лапласом ([431, с. 301 — 310]). Соответствующие графики оо и с = со/х в виде функций от и показаны на рис. 5.5.[ ...]

Рисунки к данной главе:

Плоская синусоидальная волна, движущаяся под углом к оси. Волновой вектор (£, /) имеет модуль к. Заметим, что длина волны 2л/к, наблюдаемая в разрезе по оси х, больше, чем действительная длина волны 2л/и.

Дисперсионное соотношение для поверхностных гравитационных волн на воде глубины Н. (а) Частота (о и (б) фазовая скорость с как функции волнового числа к. Пунктирная линия показывает приближение для длинных волн, когда %Н < 1, и приближение для коротких воли, когда %Н > 1. Максимальная ошибка этих приближений равна 13 % при нЯ — 1.

Движение жидких частиц в бегущей волне (а) и (б) в стоячей волне (показано стрелками). Сплошная линия показывает свободную поверхность в некоторый начальный момент, а штриховая линия показывает положение этой поверхности через некоторое малое время. Стрелки показывают перемещения частиц за это время. Для стоячей волны траектории частиц являются прямолинейными отрезками, ориентация которых зависит от положения относительно гребней. Для бегущей волны траектории частиц суть эллипсы, которые приобретают вид окружностей для больших и# и вид прямолинейных отрезков для малых кН. В каждом случае возмущенное давление является наиболее высоким под гребнем и наиболее низким под впадиной.

Вернуться к оглавлению