На протяжении этого пункта будем считать, что диссипативность решений уравнения (2.1.17) установлена (см. теоремы 2.1.10 и 2.1.17). Пусть Уо — нетривиальное стационарное решение и х0 = — С У0.[ ...]
Предложение 2.2.6. Всякое решение уравнения (2.1.17), начинающееся в Я™ 0, может находиться на конечном расстоянии от гиперплоскости (г У = хр—х0 лишь конечное время.[ ...]
Следовательно, Ь У(О растет экспоненциально. Этот факт противоречит диссипа-тивности уравнения (2.1.17). Предложение доказано.[ ...]
У (г) из Л™ 0 не стремится к У0 при г - 00, то число перемен знака скалярной функции С У (г) - С У0 стремится к бесконечности при I -+°°.[ ...]
Практическое значение данного результата сводится к тому, что в популяции с возрастной структурой, размножающейся при стационарных внешних условиях и отсутствии каких-либо периодических возмущений, суммарная численность может колебаться около некоторого постоянного уровня. При этом амплитуда колебаний не убывает со временем и может быть достаточно большой. Причиной таких колебаний является существенное различие в реакциях возрастных групп на недостаток источников питания и ограниченности жизненного пространства.[ ...]
Сформулируем результат о существовании периодического решения в строгом смысле этого слова для модели динамики численности с возрастной или фазовой структурой. Идея доказательства существования периодического решения состоит в построении выпуклого инвариантного компактного множества О, которое фазовым потоком уравнения (2.1.17) отображается в себя [29]. При построении этого множества решающую роль будет играть результат предложения 2.2.7. Неподвижная точка отображения множества О в себя, отличная от начала координат и стационарного решения У0, будет задавать начальное условие для искомого периодического движения. Существование периодического движения будет следствием соответствующего варианта теоремы о неподвижной точке [41, 49, 50].[ ...]
Введем некоторые обозначения. Через 1/(0) будет обозначать некоторую окрестность множества Д через — гиперплоскость С У = С У0. Пользуясь тем, что положительно инвариантным множеством уравнения (2.1.17) является конус У £ /? " А У> 0 , который содержит внутри себя стационарное решение У0, все условия в формулируемой ниже теореме будем считать выполненными лишь на зтом конусе.[ ...]
Тогда уравнение (2.1.17) имеет периодическое решение ненулевого периода.[ ...]
О Ф р г (s0 ) < 5 и достаточно малом е не нарушает условие неустойчивости. Предложение доказано.[ ...]
Рисунки к данной главе:
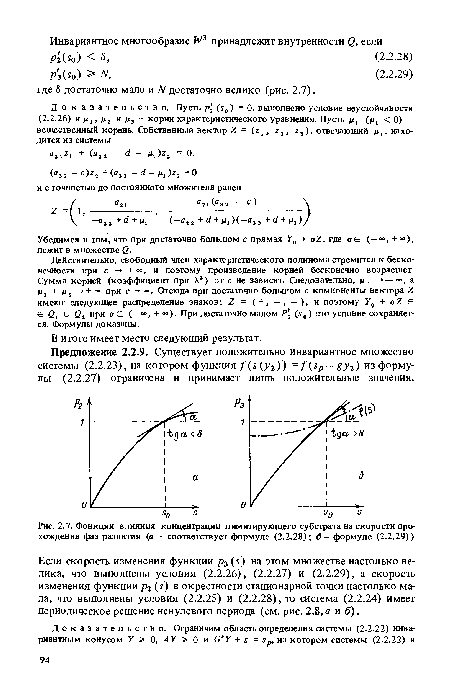
| Фонкции влияния концентрации лимитирующего субстрата на скорости прохождения фаз развития (а - соответствует формуле (2.2.28); б - формуле (2.2.29)) |
 |
| Колебания численности непрерывно культивируемой популяции почкующихся клеток |
 |