Если первая отличная от нуля величина 1р < 0, то периодическое решение асимптотически устойчиво; если 1р > 0, то неустойчиво и в обоих случаях результат существования периодического решения структурно устойчив, так как д(е) принимает значения из некоторого интервала [21]. Частота колебаний с точностью до малых величин не зависит от ляпуновской величины и приближенно равняется частоте колебаний линеаризованной системы со.[ ...]
Алгоритм вычисления ляпуновской величины состоит в проведении последовательной нелинейной замены переменных, разложении правых частей уравнения в ряды Тейлора и вычислении коэффициентов при одинаковых степенях [20, 21]. Ввиду большой трудоемкости и чрезвычайной громоздкости вычислений к настоящему времени для уравнений общего вида вычислить первую ляпуновскую величину удалось лишь для систем не выше четвертого порядка [21]. Для систем произвольной размерности это удалось сделать лишь в некоторых специальных случаях [21] либо получить алгебраическое представление /1, зависящее от величин, алгоритм вычисления которых также чрезвычайно трудоемок [21]. Величина ¡1 вычисляется через производные правой части уравнения до третьих степеней включительно и условие =£0 является ’’типичным” в С3-топологии, так как сколь угодно малые возмущения уравнений в этой топологии приводят к условию /1 0. Поэтому для практических целей знания знака /! достаточно. Формулы, приведенные в работе [21], позволяют выписать характеристики периодического решения в терминах ляпуновской величины. Воспользуемся ими в наших исследованиях.[ ...]
По-прежнему будем предполагать, что матрица В имеет пару мнимых собственных значений ± /со и остальная часть ее спектра лежит в левой полуплоскости. Обозначим через ык передаточную функцию системы (2.2.12) при наблюдении по сигналу ок(У).[ ...]
Если /1 < 0, то периодическое решение уравнения (2.2.11), лежащее в малой окрестности стационарной точки, устойчиво; если/) > 0, то неустойчиво.[ ...]
Доказательство. Проведем разложение правой части уравнения (2.2.11) в окрестности стационарной точки до полиномов третьей степени включительно. Вначале с помощью линейной замены переменных упростим линейную часть этого разложения.[ ...]
Таким образом, в первых двух уравнениях полученной системы нет линейных членов от переменных z г (f = 1,..., л).[ ...]
Отсюда — / do задается формулой (2.2.13).[ ...]
Отсюда и из формул (2.2.18) и (2.2.19) получаем окончательные выражения для вычисления параметров ляпуновской величины. Теорема доказана.[ ...]
Рисунки к данной главе:
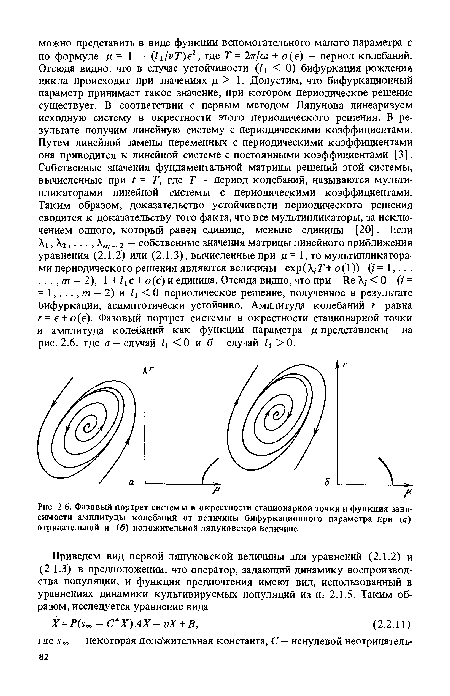
| Фазовый портрет системы в окрестности стационарной точки и функция зависимости амплитуды колебаний от величины бифуркационного параметра при (а) отрицательной и (б) положительной ляпуновской величине |
 |