При выводе дифференциального уравнения термобарических волн (223) в § 15 из уравнений движения и уравнения теплопередачи пришлось исключить те составляющие и иг?, которые характеризуют возмущение скорости потока. В результате уравнение (223) оказалось способным описать лишь поведение температуры в возмущенном поле.[ ...]
До настоящего времени никому еще не удалось проделать аналогичный вывод непосредственно для составляющих и иг;. Поэтому ограничимся лишь исследованием скоростей в возмущенном муссонном поле, исходя из заданного температурного поля, меняющегося во времени по закону, найденному Шулейкиным, в соответствии с формулой (232).[ ...]
Общие уравнения (259) и (260) совершенно аналогичны по форме дифференциальным уравнениям вынужденных колебаний для системы без затухания. Стало быть, в результате интегрирования мы должны ожидать, что обе составляющие скорости будут выражены в виде двучленов, причем один член окажется связанным с колебаниями, обладающими частотой а (частотой самих сейш), а другой, такого же порядка по величине,— с колебаниями, обладающими частотой 2о5 (удвоенной частотой вращения координатной системы). Другими словами, составляющие приращения скорости ветра (и и г?) всюду будут меняться во времени по закону (252), найденному в предыдущем параграфе для одиночной частицы, колеблющейся с большим периодом в поле кориолисовой силы.[ ...]
Но существуют ли в природе эти полусуточные колебания составляющих и иг;, требуемые теорией?—Несомненно существуют. Их давно уже подметили аэрологи как в СССР, так и за границей. В частности, на рис. 399 воспроизведены данные Зоннбликской обсерватории. Верхняя половина (4) диаграммы касается восточной слагающей ветра, а нижняя (В) — северной слагающей (обе выражены в несколько необычных единицах — километрах в час). Под ломаными линиями—результатами регистрации — помещены их разложения на основные гармоники: с периодами 12 час (сплошные кривые), 16,5 часа (частый пунктир) и 24 часа (штрих-пунктирные кривые). Кривые, суммирующие эти три слагающие, нанесены более жирными прерывистыми линиями; они воспроизводят основные черты регистрации. Легко видеть, что полусуточные составляющие достигают здесь вполне ощутимых размеров.[ ...]
Следует отметить, что действительное существование полусуточных составляющих ветра является необходимым, но еще не вполне достаточным подтверждением нашей теории. Как показано в работе [49], составляющие эти должны появляться вообще при нестационарных процессах в атмосфере. Совершенно естественно появляются они и в процессе сейш.[ ...]
Хорошее дополнительное подтверждение нашей теории сейш дают низкочастотные члены в скобках (263) и (264): легко убедиться в том, что эти члены свидетельствуют о непрерывном вращении соответствующей слагающей ветра против часовой стрелки 1 с периодом, равным периоду сейш.[ ...]
Но именно так ведет себя в действительности вся картина поля термобарических сейш, притом не только сейш в муссонном поле, но и родственных сейш, возникающих в поле межширотных тепловых потоков. Последние особенно четко подтвердили теорию во время необычайных морозов в январе 1940 г.[ ...]
Исходя из уравнений (263) и (264), легко найти траекторию воздушных частиц в поле термобарических сейш, приняв во внимание, что и представляет собой производную по времени от смещений £ воздушной частицы вдоль стационарного муссонного потока Е/, а V является аналогичной производной от смещений т] перпендикулярно тому же стационарному потоку.[ ...]
Форма этой своеобразной траектории изображена на рис. 398.[ ...]
Как видим, рассмотренный случай соответствует типичным природным условиям: исследуемая частица обходит вокруг положения покоя за 8 суток (за часто встречающийся период сейш). При этом она движется в основном против часовой стрелки. Добавочная — полусуточная — составляющая движения создает лишь своеобразные зубцы на траектории, причем в данном конкретном случае число таких зубцов должно равняться 17 + 1 = 18, так как за время 17 оборотов «спутника» сама воображаемая «планета» совершает тоже один оборот (но в противоположную сторону).[ ...]
Рисунки к данной главе:
| Самовозбуждающиеся колебания температур при конвекции |
 |
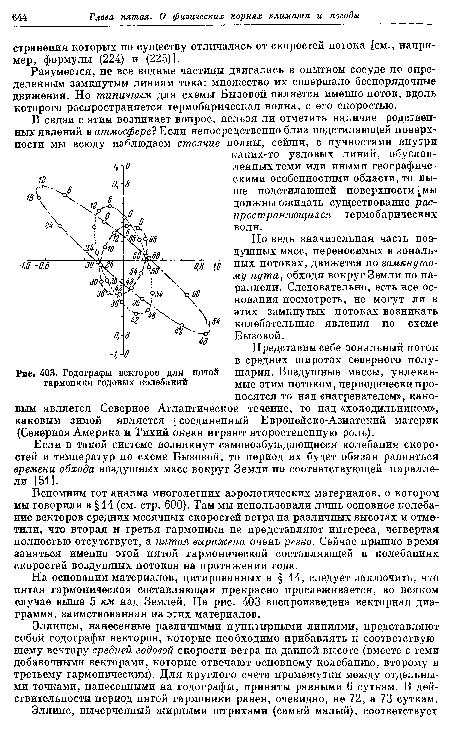
| Годографы векторов для пятой гармоники годовых колебаний |
 |