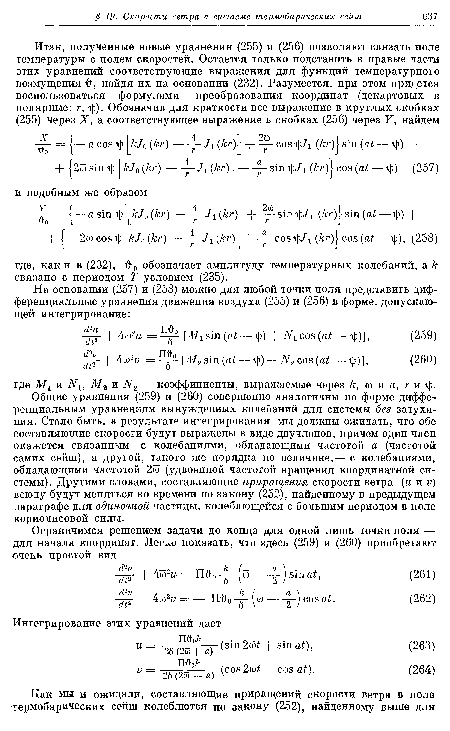
Общие уравнения (259) и (260) совершенно аналогичны по форме дифференциальным уравнениям вынужденных колебаний для системы без затухания. Стало быть, в результате интегрирования мы должны ожидать, что обе составляющие скорости будут выражены в виде двучленов, причем один член окажется связанным с колебаниями, обладающими частотой а (частотой самих сейш), а другой, такого же порядка по величине,— с колебаниями, обладающими частотой 2о5 (удвоенной частотой вращения координатной системы). Другими словами, составляющие приращения скорости ветра (и и г?) всюду будут меняться во времени по закону (252), найденному в предыдущем параграфе для одиночной частицы, колеблющейся с большим периодом в поле кориолисовой силы.
Скачать страницу
[Выходные данные]