Общее дифференциальное уравнение полного энергетического баланса волн в любой точке мелководного моря должно содержать еще один дополнительный член по сравнению с уравнением (235), записанным для района, удаленного от наветренного берега. Этот дополнительный член учтет «высасывание» энергии волн, о котором уже говорилось применительно к океанским условиям [см. выше, формулу (220)].[ ...]
Здесь Н—глубина мелководного моря.[ ...]
Как видим, в отличие от формулы (220), сюда вошла глубина моря Н, а полу-высота волн г здесь входит в первой степени вместо степени 5/2.[ ...]
После нахождения точного интеграла поля ветровых волн в океане пррь ведем точное решение задачи для столь мелководного моря, что вполне законными являются и формула (243), и равенство Нг = Н, заменяющее сложную формулу (232). Столь же законным будет пренебрежение потерями энергии на внутреннее турбулентное трение по сравнению с потерями на частичное разрушение вершин волн под действием мелководья.[ ...]
Легко видеть, что по прошествии очень большого срока работы ветра обращается в нуль левая часть равенства (246), а на достаточно большом расстоянии от наветренного берега становится равным нулю последний член правой части (246). При этом полувысота волн г достигает своего наибольшего значения г2, возможного на море с глубиной Н при относительной скорости ветра (V — с).[ ...]
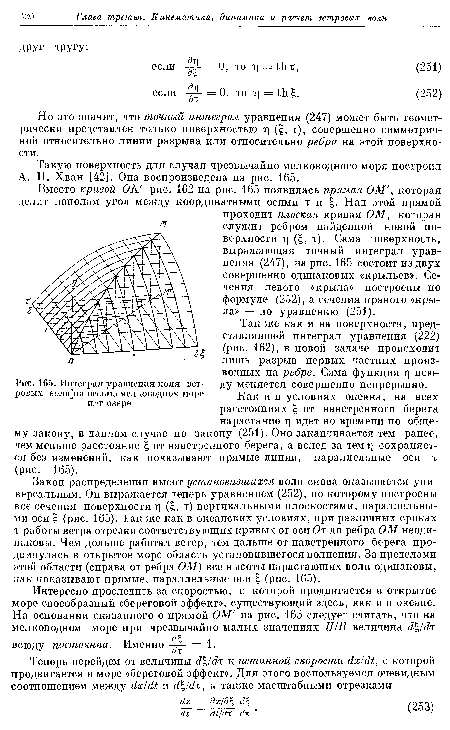
Но это значит, что точный интеграл уравнения (247) может быть геометрически представлен только поверхностью ц (£, т), совершенно симметричной относительно линии разрыва или относительно ребра на этой поверхности.[ ...]
А. П. Хван [42]. Она воспроизведена на рис. 165.[ ...]
Так же как и на поверхности, представлявшей интеграл уравнения (222) (рис. 162), в новой задаче происходит лишь разрыв первых частных производных на ребре. Сама функция т] всюду меняется совершенно непрерывно.[ ...]
Как и в условиях океана, на всех расстояниях £ от наветренного берега нарастание г идет во времени по общему закону, в данном случае по закону (251). Оно заканчивается тем ранее, чем меньше расстояние от наветренного берега, а вслед за темт] сохраняется без изменений, как показывают прямые линии, параллельные оси т (рис. 165).[ ...]
Закон распределения высот установившихся волн снова оказывается универсальным. Он выражается теперь уравнением (252), по которому построены все сечения поверхности т] (£, т) вертикальными плоскостями, параллельными оси (рис. 165). Так же как в океанских условиях, при различных сроках т работы ветра отрезки соответствующих кривых от оси Ох до ребра ОМ неодинаковы. Чем дольше работал ветер, тем дальше от наветренного берега продвинулась в открытое море область установившегося волнения. За пределами этой области (справа от ребра ОМ) все высоты нарастающих волн одинаковы, как показывают прямые, параллельные оси £ (рис. 165).[ ...]
Рисунки к данной главе:
| Интеграл уравнения поля ветровых волн^на весьма мелководном море |
 |