Число оборотов оси обтюратора в единицу времени известно. Следовательно, известны промежутки времени, отделяющие одно положение фонарика на траектории от другого, соседнего.[ ...]
На рис. 133 изображена траектория фонарика-поплавка, зарегистрированная при одном из опытов. Кружочками отмечены середины отрезков, полученных на фотографии в те промежутки времени, когда обтюратор открывал доступ света в объектив прибора. Вместо замкнутой орбиты создалась сложная траектория с петлями: на круговращательное движение, рассматриваемое в элементарной теории трохоидальных волн, наложилось поступательное движение, вызванное эффектом Стокса («волновое» течение) и, кроме того, еще усиленное благодаря дрейфу под действием ветра.[ ...]
Непостоянство параметров волн, следующих одна за другой в экспериментальном бассейне, затрудняет обработку таких регистраций и выделение чисто орбитального движения. Однако большая серия опытов позволила установить несомненное наличие одного из двух явлений: а) если считать скорость «волнового» стоксова течения и скорость дрейфового течения постоянными в продолжение одного периода волн, то необходимо признать переменной угловую скорость орбитального движения частиц; б) если принять угловую скорость орбитального движения постоянной, то необходимо отказаться от установившегося представления о постоянстве стоксова течения и течения дрейфового,— необходимо заключить, что и та и другая составляющие поступательного движения пульсируют в пределах одного периода волн.[ ...]
Легко видеть, что первый вариант несовместим с принципами динамики. Ведь заостренная форма волн, при соответствующей их крутизне, возможна и в отсутствие ветра, а следовательно, при полном отсутствии внешних действующих сил; между тем всякое изменение угловой скорости орбитального движения может возникать лишь под воздействием каких-то внешних сил. Значит, необходимо остановить внимание на втором варианте и, рассмотрев его, выяснить физические причины заострения вершин волн конечной крутизны.[ ...]
Нетрудно заметить, что при подстановке в уравнение (68) частного значения у — 0 (для поверхностных частиц) получается та же самая величина. Напомним, что через с обозначена фазовая скорость волн относительно водных масс.[ ...]
Как видим, эллипс растягивается тем больше, чем больше крутизна волн, непосредственно связанная с г0Ш, и чем больше отношение осредненной скорости дрейфового течения й к скорости орбитального движения и.[ ...]
Формула (89) дает применительно к такому случаю] = 1,45.[ ...]
До сих пор говорилось о движении водных частиц на самой поверхности моря. Можно добавить, что под й подразумевалась та составляющая дрейфового течения (осредненная), которая направлена в сторону распространения волн, т. е. в сторону движения воздушного потока над морем. Составляющая дрейфового течения, нормальная к ней, не может менять исследуемый профиль одномерной волны; однако она должна отражаться на профилях трехмерных волн, полученных при пересечении взволнованной поверхности с вертикальной плоскостью, нормальной к направлению ветра. К этому обстоятельству, вероятно, вернутся исследователи, когда физика трехмерных волн получит достаточное развитие.[ ...]
В свое время В. В. Шулейкин сделал попытку вычислить отношение между амплитудой заостренных волн, измеренной на поверхности моря, и амплитудой вертикальных колебаний водных частиц на глубинах — до самого дна (в случае не слишком глубокого моря, где регистрация волн ведется на придонных волнографах). Анализ указал на наличие «фильтрации» высоких гармоник, налагающихся на основное колебание частиц. В связи с этим, во-первых, получило объяснение почти чисто синусоидальное очертание профилей, зарегистрированных на глубинах, при наличии сильно заостренных профилей волн на поверхности моря; во-вторых, было показано, что амплитуда волн должна на глубинах уменьшаться быстрей, чем вытекает из классической теории трохоидалъных волн. Но многочисленные измерения амплитуд на глубинах, в особенности тщательные измерения, произведенные JI. А. Корневой и в море, и в штормовом бассейне, обнаружили, что в действительности амплитуды колебаний давления на глубинах уменьшаются еще быстрей, чем вытекает из анализа «фильтрации» гармоник. Интересно, что расхождение не увеличивается стремительно при переходе ко все большим и большим глубинам: это расхождение ограничено каким-то пределом [2]. Поэтому представляет интерес новый анализ явления, произведенный совсем иным путем [9].[ ...]
Запишем условие неразрывности в форме Лагранжа (2), отметив, что само уравнение (2) содержит вместо принятых буквенных обозначений а, 3 обозначения а, Ь, неудобные сейчас ввиду того, что этими буквами обозначаются полуоси эллипса.[ ...]
Рисунки к данной главе:
| Траектория фонарика-поплавка |
 |
| Схемы для выяснения природы волнового |
 |
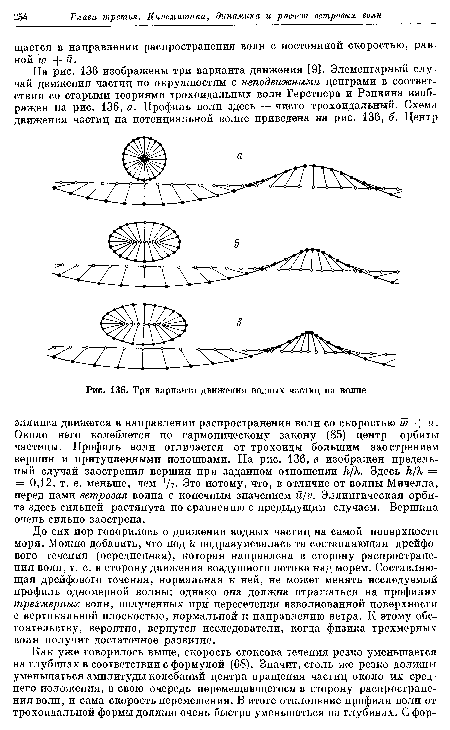
| Три варианта движения водных частиц на волне |
 |