Морские течения рассматривались до сих пор на основе первой схемыг упомянутой в § 8: всюду молчаливо допускалось, что среди сил внутреннего трения преобладают силы, возникающие между горизонтальными слоями; всюду исключались из рассмотрения те силы трения, которые могут возникать на вертикальных границах водных масс, исключались из анализа силы «бокового трения» в воде.[ ...]
Как говорилось в § 8, первая схема позволяет решить до конца (до числа) задачи о распределении скоростей течения как по горизонтальным, так и по вертикальному направлению; в большинстве случаев это не представляет особого труда, так как с формальной стороны эти задачи аналогичны давно решенным задачам о поле логарифмического потенциала.[ ...]
К сожалению, подобное решение связано с большими погрешностями, когда в океане существует очень большой градиент плотности вод по вертикали. В этих случаях сильно затрудняется перемешивание между горизонтальными слоями и снижается величина коэффициента турбулентного трения между ними; коэффициент бокового трения здесь может превысить в 106 и даже в 107 раз величину коэффициента межслойного трения. Следовательно, даже при сравнительно небольших значениях горизонтального градиента скоростей произведение этого градиента на коэффициент бокового трения может значительно превысить произведение вертикального градиента скоростей на коэффициент межслойного трения. Другими словами, силы бокового трения здесь должны играть большую роль по сравнению с силами межслойного трения. При наличии очень большой глубины океана в соответствующем районе, придется признать, что трение вод о дно пренебрежимо мало по сравнению с трением между водами исследуемого потока и окружающей водной средой по бокам потока. Значит, для возможно большего приближения к истине здесь надо по-новому схематизировать картину потоков, выдвинув на передний план влияние бокового трения.[ ...]
До настоящего времени эта, вторая, схема потоков позволила решить сравнительно ограниченное число задач и притом решить их, как правило, лишь в обобщенном виде —в виде уравнений, описывающих результирующие потоки.[ ...]
В нашей стране такие задачи решил В. Б. Штокман, с работами которого следует познакомиться всем интересующимся морскими течениями как с теоретической, так и с практической стороны. Здесь мы изложим основные мысли этого автора [29].[ ...]
Умножим все члены уравнений на толщину йъ элементарного слоя и проинтегрируем каждый член полученного нового уравнения по вертикали в пределах от ъ = 0 до г = Н, где Н — глубина океана в исследуемой точке.[ ...]
Отметим, что при интегрировании величина б была заменена некоторой средней величиной плотности, так как составляющие скорости или меняются по вертикали значительно быстрей, чем меняется б.[ ...]
Любопытно, что уравнение (279) по своей форме совершенно аналогично уравнению изгиба пластины под действием приложенных к ней сил, широко применяемому при решении задач теории упругости. Функция потока здесь играет формально ту же роль, какую в упругостных задачах играет прогиб пластины; роль величины rotz Т здесь та же, что и у нагрузки, приложенной к пластине; коэффициент бокового турбулентного трения формально занимает то же место, что и коэффициент цилиндрической жесткости пластины в упругостных задачах.[ ...]
Как известно, решение задач теории упругости обычно бывает более сложным по сравнению с задачами гидродинамики, связанными с интегрированием уравнений в частных производных лишь второго порядка: на сцену вступают уравнения в частных производных четвертого порядка. Именно этим объясняется также и трудность решения до конца задач о мор-ских течениях, связанных с учетом бокового трения; мы видели, что уравнение Штокмана (279) содержит частные производные четвертого порядка.[ ...]
Те же осложнения встречаются на пути исследования полей масс, связанных с полем ветра. В этой области основные соотношения были получены тем же автором. Воспроизводя их вывод, прежде всего выразим составляющую потока х из второго уравнения системы (272).[ ...]
Рисунки к данной главе:
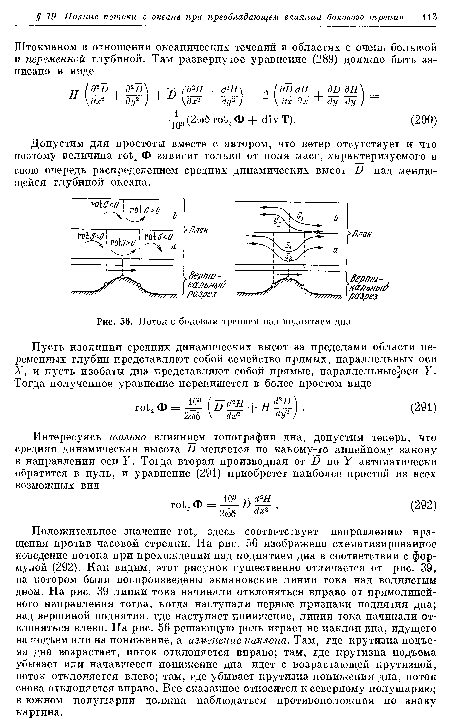
| Поток с боковым трением над поднятием дна |
 |