Вернемся снова к замкнутой трофической цепи и зададимся вопросом: а сохранится ли стохастичность при увеличении длины цепи? Но прежде чем ответить на этот вопрос, необходимо рассмотреть некоторые общие математические концепции.[ ...]
Предположим далее (достаточно стандартные предположения) следующее.[ ...]
Пусть вырожденная система (5.3) имеет гиперболическое множество АСИ СИ СУ. Будет ли тогда сингулярно возмущенная система (5.1) обладать гиперболическим множеством? Оказывается, что имеет место следующее утверждение.[ ...]
Ре, порождаемый системой (5.1), имеет гиперболическое множество Л6 CR" + "1, близкое к А и топологически эквивалентное (сопряженное) ему.[ ...]
Вернемся снова к трофическим цепям. В § 2 этой главы было показано, что трофическая цепь длины три при соответствующих значениях параметра С имеет странный аттрактор в R3, образованный в результате последовательных удвоений циклов. Предположим, что возникший после завершения бесконечной цепочки удвоений при С € (См, С» + S) этот странный аттрактор имеет гиперболическую структуру, т.е. является гиперболическим множеством. Это предположение, означающее грубость движения на странном аттракторе, очень естественно в экологических задачах.[ ...]
Предположим теперь, что мы умеем находить условия, накладываемые на параметры системы (5.4), размерности п — 1, а не п, при выполнении которых эта система имеет гиперболическое множество в И"-1 (точнее, в положительном ортанте Рп 1). С другой стороны, заметим, что вырожденная система (1у1 = = 6(0, 1р(у), у) отличается от системы (5.4) размерности п — 1 только сдвигом индексов. А поскольку мы предположили существование у последней гиперболического множества, то выполнено и последнее, третье условие.[ ...]
Тогда, согласно сформулированному выше утверждению, найдется такое е0 > 0, что для всех е€ (0, е0) система (5.4), но уже размерности и, т.е. трофическая цепь длины и, будет иметь гиперболическое множество Ле, близкое к Л и сопряженное ему.[ ...]
Из существования гиперболического странного аттрактора для системы (2.1) в Р3 (или для системы (5.4) при п = 3) следует существование аттрактора для системы (5.4) при и = 4 (в ?4) и т.д. Другими словами, из существования стохастического режима в замкнутой трофической цепи длины три следует возможность возникновения стохастических режимов в цепях произвольной длины, большей чем три.[ ...]
Хотя в начале главы мы и говорили, что не будем касаться дискретных популяционных моделей с хаотическим поведением, тем не менеё для демонстрации весьма интересного явления мы нарушим это соглашение.[ ...]
Здесь е [0,1] - доля отбираемой биомассы (или численности), Т — фиксировано.[ ...]
Рисунки к данной главе:
| Понижение равновесной численности при введении оптимального урожая (N - 4 708) для риккеровской модели при г = 1,1 и N° = 1 |
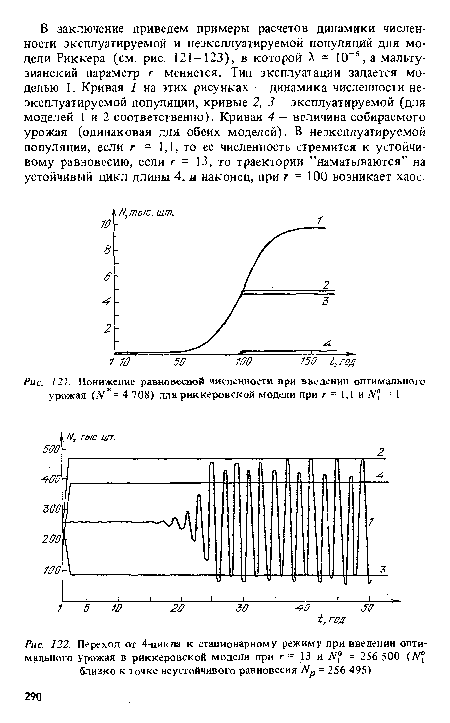 |
| Переход от 4-цикла к стационарному режиму при введении оптимального урожая в риккеровской модели при г = 13 и N° = 256 500 (№1 близко к точке неустойчивого равновесия = 256 495) |
 |
| Ликвидация "хаоса” при введении оптимального урожая в рикке-ровской модели при г = 100 и N° = 460 516 (точка неустойчивого равновесия = 460 517) |
 |