Наглядным критерием стохастичности служит метрическая энтропия, характеризующая среднюю скорость разбегания траекторий и сложность всей системы в целом. Так как точно определить значение энтропии в реальной ситуации практически невозможно, приведем здесь лишь формулу для ее приближенного вычисления. Точнее говоря, по этой формуле вычисляется максимальный показатель Ляпунова (а), положительность которого свидетельствует и о положительности колмогоровской энтропии.[ ...]
На рис. 113—115 приведены проекции интегральных кривых системы (2.1) на координатные плоскрсти. Из рисунков хорошо видны результаты последовательных бифуркаций удвоения, а также процесс приближения непериодической траектории к странному аттрактору.[ ...]
Кроме того, из экологических соображений кх,кх < 1. Другими словами, здесь допускается, что при переходе с одного уровня на другой может происходить потеря вещества, но так, что общее количество вещества в системе не меняется.[ ...]
Так как по смыслу самой задачи — замкнутость экосистемы — следует ограниченность траекторий (4.1), то наличие неустойчивого нетривиального равновесия указывает на возможность существования у системы сложных динамических режимов — циклов и хаоса.[ ...]
На плоскости оставшихся свободными двух параметров а и С можно построить области, соответствующие различным динамическим режимам (см. рис. 117). Например, из неравенства (4.3) в этом случае следует, что нетривиальное равновесие существует, если параметры а и С лежат выше кривой АВС, и оно устойчиво, если эти параметры лежат в заштрихованных областях. Когда при изменении параметров точка (а, С) пересекает границы областей устойчивости, то возникает типичная ситуация рождения цикла в результате бифуркации Андронова — Хопфа. При дальнейшем движении точки к затемненным областям происходит удвоение циклов, и наконец, при значениях параметров а и С из ’’темных” областей в системе возникает хаос.[ ...]
Численное исследование изменения малого объема фазового пространства 5 Г вдоль траекторий нашей системы для случая а = 0,225; С = 20 показало, что при г 6Г(г) е 33г,т.е. наша система является диссипативной, а мера странного аттрактора в К4 равна нулю.[ ...]
И наконец, численная оценка колмогоровской энтропии для системы (4.1) показала, что при t - ■ °° а - ■ ст» >,0,02, т.е. опять же имеем дело с хаотическим режимом.[ ...]
На рис. 120 изображена проекция интегральных кривых (4.1) на плоскость N2 = const. Хорошо видна структура странного аттрактора и характер приближения траекторий к нему.[ ...]
Рисунки к данной главе:
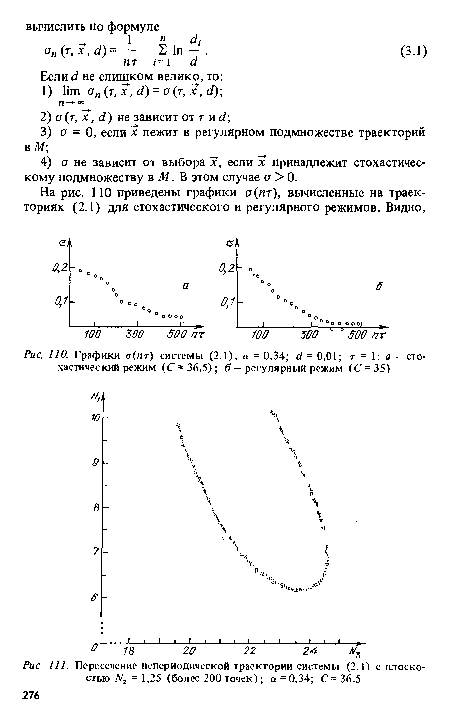
| Графики о (пт) системы (2.1), а = 0,34; <1 = 0,01; т = 1 |
 |
| Пересечение непериодической траектории системы (2.1) с плоскостью Ыг - 1,25 (более 200точек); а = 0,34; С= 36,5 |
 |
| График функции 5 (?) системы |
 |
| Области различных динамических режимов для системы (4.1) |
 |
| Картина отображений Пуанкаре для системы (4.1). Четные (о) и нечетные ( X ) отображения |
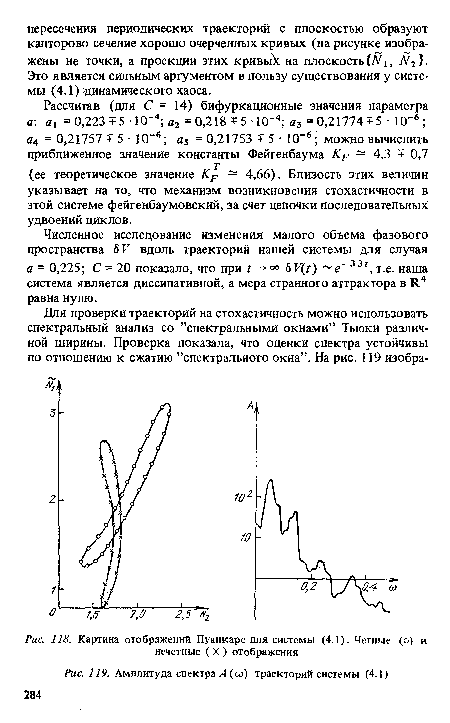 |
| Амплитуда спектра A(oj) траекторий системы (4.1) |
 |