Эти условия описывают ситуацию, когда только на определенном участке есть растительность, а где-то далеко в верхнем течении реки постоянно сбрасываются загрязнения, так что, несмотря на унос с течением, там поддерживается постоянная концентрация загрязнений.[ ...]
Ясно, что при R > R G(R) > 0, причем она монотонно возрастает с ростом R.[ ...]
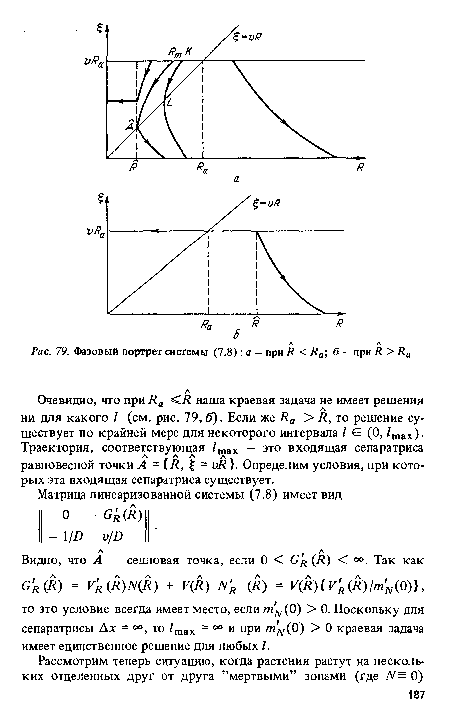
Очевидно, что траектории, удовлетворяющие граничному условию (7.4), должны начинаться на горизонтальной прямой £ = vRa, а условию (7.5) - заканчиваться на прямой £ = иЛ (рис. 79, а, б).[ ...]
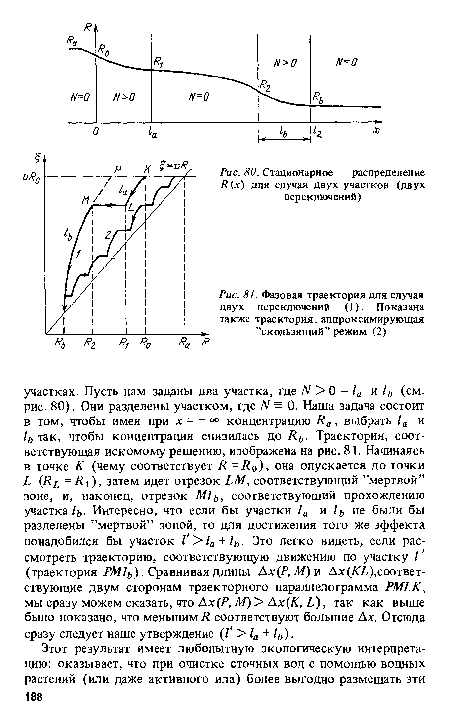
Таким образом, длина отрезка Дл:, на котором происходит переход системы (7.8) с горизонтальной прямой £ = и/?а на прямую £ = и/?, возрастает по мере перемещения траекторий в сторону меньших значений R (к < R < Ra). Аналогичный результат имеет место и при R > Иа, ко здесь переход происходит с одной горизонтали на другую.[ ...]
Возвращаясь опять к рис. 81, можно видеть, что этот эффект тем сильнее, чем ближе траектория с переключениями лежит к прямой £ = vR. Можно показать, что максимальный эффект достигается лишь в ’’скользящем” режиме при бесконечном числе переключений.[ ...]
Так как WЛ > 0, то отсюда сразу следует устойчивость (по Ляпунову) построенных стационарных решений.[ ...]
По-видимому, этим можно закончить как описание некоторых методов построения диссипативных структур, так и конкретных их примеров. Правда, некоторая интересная информация, имеющая отношение к диссипативным структурам, будет еще сообщена в следующей главе. А здесь мне бы хотелось остановиться на одной гипотезе, надеясь, что она стимулирует развитие исследований в этом направлении.[ ...]
Как до сих пор в основном развивались исследования по диссипативным структурам? Шли по пути как увеличения числа уравнений типа ’’реакция — диффузия”, так и по пути все более усложненного (более ’’нелинейного”) описания локальных взаимодействий. Форма областей же, в которых искались диссипативные структуры, оставались простыми и примитивными (на плоскости -- прямоугольник, круг). Но в окружающей нас природе эти формы встречаются крайне редко. Достаточно взглянуть на карты ареалов распространения различных видов (или популяций) растений или животных — до чего же причудливыми бывают их границы. Или излюбленный процесс ученых, занимающихся диссипативными структурами — морфогенез. Ведь только лишь на самых первых стадиях развивающийся организм имеет простую форму, затем формы резко усложняются. Заметим, кстати, что основное топологическое свойство простых форм, используемых в теории (круга, прямоугольника) - выпуклость, очень редко присуще реальным формам живой природы (будь то ареал обитания или развивающийся организм) . С другой стороны, в § 3 было показано, что даже простая система, динамика которой описывается одним уравнением, но в сложной области, где нарушено условие выпуклости, порождает диссипативную структуру. Заметим, что та же самая система, но помещенная в простую область диссипативной структуры, не порождает.[ ...]
Рисунки к данной главе:
| Зависимость функции смертности потребителя от его численности |
 |
| Возможный вид стационарного распределения ресурса R(x) |
 |
| Фазовый портрет системы (7.8) |
 |
| Фазовая траектория для случая двух переключений (1). Показана также траектория, аппроксимирующая "скользящий” режим (2) |
 |