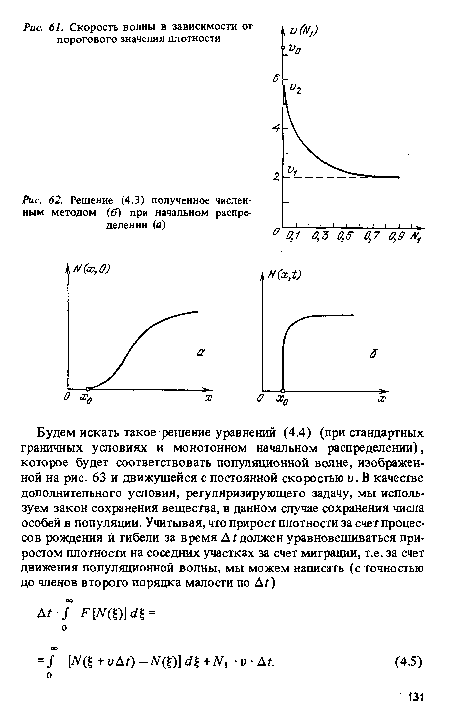
Изображенная на рис. 61 зависимость v Nx) может быть весьма полезной для практического отыскания критического значения плотности Ni, поскольку скорость распространения волны измерить гораздо легче, чем характеристики подвижности особей.[ ...]
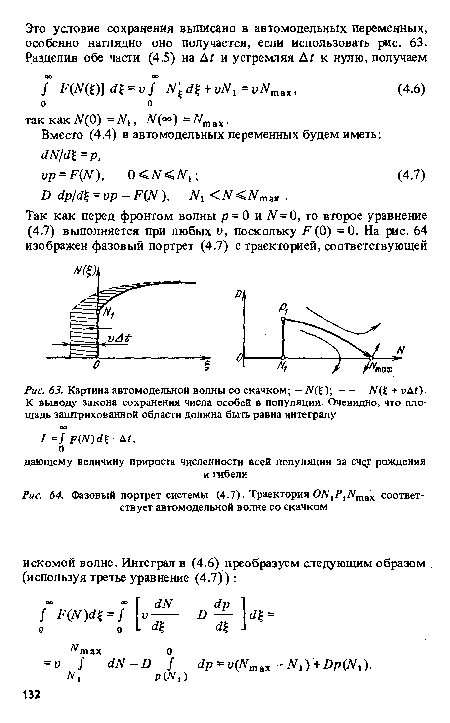
Граничные условия выбираются стандартно, как во всех волновых задачах. Численный счет с монотонным начальным распределением (см. рис. 62,а) дает решение, изображенное на рис. 62,6). Видно, что это никак не может быть движущейся волной. Однако из биологических соображений ясно, что популяция должна расселяться и распределение М(х, ?) должно смещаться влево с ростом Это противоречие объясняется неединственностью решения (4.4), которое порождается некорректностью поставленной задачи. Для того чтобы задача стала корректной,нужно задать еще одно условие, выполнение которого, в свою очередь, определит скорость волны.[ ...]
Пользуясь этой формулой, всегда можно численно найти скорость, с которой будет распространяться нерегулярная волна со скачком плотности.[ ...]
Ясно, что чем ближе пороговое значение плотности к максимальному, тем медленнее распространяется волна. С другой стороны, чем круче подходит (УУ) к максимальному значению плотности, тем больше скорость волны.[ ...]
Заканчивая этот параграф, можно сказать, что теории нерегулярных волн практически не существует, но уже по этим частным результатам видно, что здесь можно ожидать весьма интересных эффектов.[ ...]
Рисунки к данной главе:
| Картина автомодельной волны с изломом |
 |
| Решение (4.3) полученное численным методом (б) при начальном распределении (а) |
 |
| Картина автомодельной волны со скачком; - ЩЧУ,---N(4 + иДГ). |
 |
| Фазовый портрет системы (4.7). Траектория ОИ1Р1Итлх соответствует автомодельной волне со скачком |
 |