Экология СПРАВОЧНИК

Подобное распределение подтверждается для многих совершенно разных групп организмов, если только выборка достаточно велика, чтобы в нее входил класс модального обилия (обычно > 100 видов). Оно обнаружено у птиц [255], диатомовых водорослей [206], пчел и цветковых растений [256], муравьев [242]; в настоящее время установлено, что такое распределение является общим правилом для выборок большого числа таксономически близких видов [210]. Дисперсия кривых (а) довольно сходна для разных групп организмов (например, 2—3 для птиц, 3,1—4,7 для бабочек) [254]. Ее значения неодинаковы для разных сред; например, для лесных птиц на низменностях в тропиках а = 0,98, в умеренных областях— 1,36, а на островах— 1,97 [224]. Точно так же, для диатомовых водорослей в различных реках на материке и на островах о колеблется от 2,49 до 5,1 [206]. Результаты этих двух исследований позволяют считать, что на островах меньше видов, встречающихся с умеренной частотой, и больше обильных видов, чем на материках, подтверждая тем самым идеи, обсуждавшиеся в гл. 3.[ ...]

Эти модели не допускают динамического перехода видов из одного октета в другой и основаны на предположении, что вероятностные плотности обилия у всех видов одинаковы, т. е. что они симметричны. В качестве альтернативы Агленд и Грей [257] описали асимметричную модель. Большинство сообществ имеет пятнистую структуру, и частотное распределение видов в пределах каждого отдельного пятна непредсказуемо, однако оно стабилизируется для сообщества в целом, если суммировать все пятна. В этой модели принято допущение, что составляющие сообщество виды делятся по обилию на три группы — редкие (65%), промежуточные (25%) и обычные (10%), причем в пределах каждой группы соотношение видов по обилию симметрично. Из суммы таких симметричных моделей строится асимметричная модель, обеспечивающая хорошее совпадение с логарифмически нормальным распределением, которое, таким образом, основано на чисто статистических закономерностях. Подобная подгонка описывает состояние равновесия в пределах сообщества (одно из многих возможных состояний), являющееся динамическим. Например, данные за четыре года по морским бентосным сообществам хорошо соответствуют логарифмически нормальному распределению, несмотря на то, что каждый год доминирующее положение занимали разные виды [257]. Эта модель применима лишь к большим выборкам, в которых распределение обилия суммируется по многим пятнам, однако она не дает какого-либо обоснованного биологического объяснения такому распределению.[ ...]

Рисунки к данной главе:

Примеры логарифмически нормального распределения обилия видов, обнаруженного на основании

Каноническое логарифмически нормальное распределение для ассамблей из 178 видов птиц, построенное таким образом, чтобы средняя точка совпадала с нулем (1 — виды; II — особи [255]).

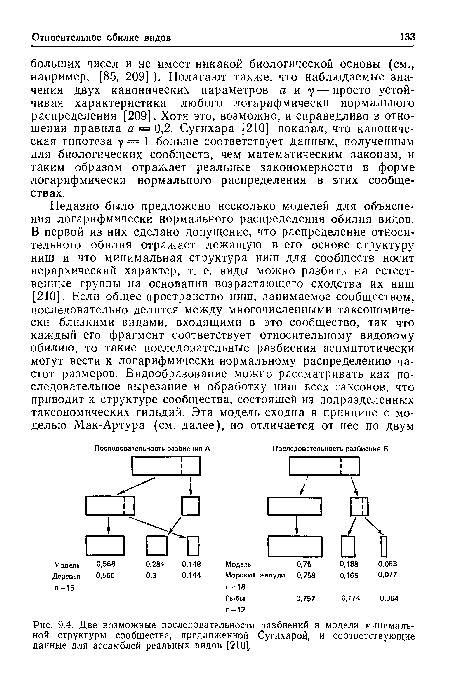
Две возможные последовательности разбиений в модели минимальной структуры сообщества, предложенной Сугихарой, и соответствующие данные для ассамблей реальных видов [2101.