Лоренц принял также соглашение, что давление на любой изэнтропической поверхности, которая пересекает поверхность земли, равно давлению в точке пересечения. Он показал также, что для малых возмущений это приводит к формулам, полученным в разд. 6.18 с использованием изобарических координат. Это связано с тем, что в основу расчетов положено гидростатическое приближение. Однако Лоренц не рассматривал подробно вклада эффектов на поверхности. Обсуждение этого вопроса можно найти в [181].[ ...]
Этот раздел посвящен понятию завихренности и его связи с циркуляцией.[ ...]
Таким образом, движение в окрестности жидкой частицы можно всегда разложить на две части, каждая из которых соответствует одному из членов правой части (7.9,7). Вторая часть представляет собой (см. (4.5.2)) чистое вращение с угловой скоростью £/2, что объясняет, почему £/2 отождествляется с локальной скоростью вращения жидких элементов. В старых работах для этой величины использовались такие названия, как «угловая скорость» или «вращательная скорость». Движение, соответствующее члену (1/2)Уб(3, получается вследствие того факта, что изолинии 6 являются эллипсоидальными поверхно-. стями, так что движение, связанное с этим членом, нормально к этим поверхностям. В частности, движение вдоль осей эллипсоида линейно, а поверхность, которая в начальный момент была сферической, будет искривляться по этим осям и становиться эллипсоидальной. Это движение называется движением чисто деформационным. Таким образом, равенство (7.9.7) показывает, что движение в окрестности жидкой частицы можно всегда представить как сумму деформационного движения и чистого вращения. Более подробное обсуждение имеется, например, в [47, разд. 2.3].[ ...]
Можно увидеть (см. разд. 4.5), что эта формула предвосхищает результат Кориолиса [138] для компонент ускорения относительно системы отсчета, вращающейся вместе с жидкостью.[ ...]
Выводы Гельмгольца следуют из уравнения (7.9.13), так как оно имеет ту же форму, что и уравнение (7.9.6), для объекта, который можно назвать линейным материальным элементом бх. Из него следует, что материальный линейный элемент, параллельный в начальный момент вектору завихренности £, будет совпадать с ним по направлению и в последующие времена. Гельмгольц выразил эту идею, введя понятие вихревой нити, т. е. такой состоящей из материальных частиц линии, что касательная к ней в каждой точке направлена вдоль завихренности. Так как каждый сегмент нити остается материальным линейным элементом, то отсюда следует положение Гельмгольца о сохранении вихревой нити.[ ...]
Иначе говоря, бх (и, следовательно, %) постоянна для фиксированной частицы. Результат Гельмгольца можно выразить и так: величина £/р меняется пропорционально изменению длины локального сегмента вихревой нити.[ ...]
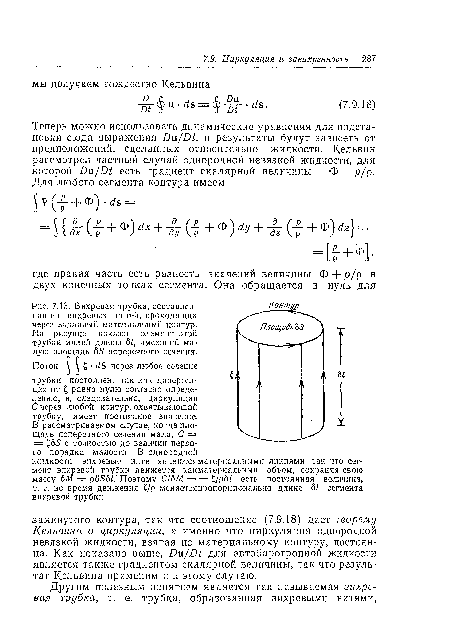
На рисунке показан элемент этой трубки малой длины öl, имеющий малую площадь 65 поперечного сечения.[ ...]
Рисунки к данной главе:
| Вихревая трубка, составленная из вихревых нитей, проходящих через заданный материальный коитур. |
 |