Экология СПРАВОЧНИК

Когда справедливо гидростатическое уравнение, т. е. горизонтальные масштабы велики по сравнению с вертикальными, то часто целесообразно вместо высоты использовать давление в качестве независимой переменной. В частности, уравнение неразрывности при этом имеет простой вид даже для сжимаемой жидкости: Уравнения в изобарических координатах получены в разд. 6.17 и используются в книге позже, в частности в связи С процессами медленного приспособления в атмосфере (гл. 12). Энергетические уравнения в этих координатах рассмотрены в разд. 6.18.[ ...]

В качестве первого примера эффектов стратификации рассмотрим случай двух жидкостей различной плотности, которые несмешиваемы или для которых эффектом смешивания можно пренебречь. Такую систему легко получить в лабораторных условиях; эксперимент Марсильи был первым примером этой системы. Гидростатическая аппроксимация будет предполагаться с самого начала, поэтому результаты должны применяться только к случаям, в которых горизонтальный масштаб велик по сравнению с глубиной. Эту задачу впервые изучил Стокс (1847) [747].[ ...]

Здесь было использовано (6.2.8).[ ...]

Приспособление системы, состоящей из двух жидкостей, таким образом, определяется уравнениями (6.2.5) и (6.2.10). Если, скажем, г] было бы исключено из них, то получилось бы уравнение в частных производных четвертого порядка относительно Н. Однако задачу можно сильно упростить, отыскивая решения со специальной структурой, а именно решения, для которых т) и /г пропорциональны, т. е.[ ...]

Это упрощение является примером метода, который может быть использован для широкого класса задач механики, описывающих малые осцилляции. Действительно, Лэмб (1932) [429] в курсе гидродинамики отводит первый раздел главы о приливных волнах изложению общей теории этого приема из-за его широкой применимости. Для настоящей задачи существуют два значения се и поэтому два значения х, которые удовлетворяют полученному уравнению. Движения, соответствующие этим частным значениям, называются нормальными модами колебаний. В системе, состоящей из п слоев различной плотности, существует п таких мод, соответствующих п степеням свободы. Непрерывно стратифицированной жидкости соответствует бесконечное число слоев, и поэтому существует бесконечное множество мод. То, что каждая из этих мод ведет себя независимо, очень удобно, и это свойство будет неоднократно использоваться. Независимость каждой моды можно видеть из того, что если к и удовлетворяли (6.2.11) в некоторый начальный момент, то они будут удовлетворять (6.2.11) и для всех последующих времен, поэтому будут происходить колебания только с одной модой, С другой стороны, любое данное начальное состояние можно представить как сумму мод, изменение каждой из которых во времени и пространстве происходит независимо от другой.[ ...]

Состояние жидкости можно тогда получить суммированием всех мод.[ ...]

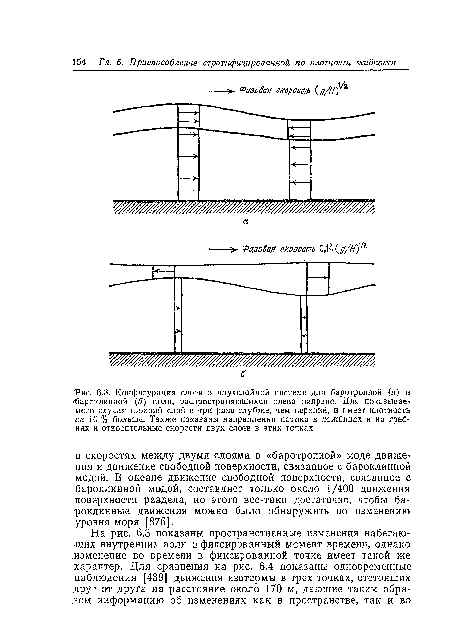
В пределе £У£- -0 это приводит к поверхностной гравитационной волне, полученной для однородной жидкости. Ее часто называют баротропной модой. Точное значение термина «баротроп-ный» состоит в том, что давление постоянно на поверхностях постоянной плотности, следовательно, постоянно на поверхности раздела. Это верно только приблизительно, тем не менее эту моду принято называть баротропной.[ ...]

Тогда внутренняя волна будет точно такой же, какой была бы поверхностная гравитационная волна, если бы ускорение силы тяжести равнялось ц вместо g. Это следует из того, что именно g/, а не g определяет теперь разность давлений (см. разд. 5.1).[ ...]

Так как £ <С g, волновая скорость внутренних волн гораздо меньше, чем волновая скорость поверхностных воли, так что внутренние волны выглядят как поверхностные волны в медленном движении. Это различие объясняет явление, упомянутое Б. Франклином ([219], стр. 438) в письме от 1 декабря 1762 г.[ ...]

Эксперимент Франклина можно поставить на кухне за минуту или две, и читателям предлагается проделать его. Инструкции даны в следующем абзаце (стр. 439) письма Франклина.[ ...]

Рисунки к данной главе:

Система обозначений, используемых для описания движения двух наложенных друг на друга мелких однородных слоев жидкости. Ни #2 — глубины слоев, когда жидкость находится в покое

Конфигурация слоев в двухслойной системе для баротропной (а) и ^бароклинной (б) волн, распространяющихся слева направо. Для показываемого случая нижний слой в три раза глубже, чем верхний, и имеет плотность на 10 % больше. Также показаны направления потока в ложбинах и на гребнях и относительные скорости двух слоев в этих точках.

Наблюдения прогрессивных внутренних волн в 20 м слое воды в 1,3 км от берега в Сан-Диего. Регистрация происходит в трех точках треугольника С, как показано на рисунке, стороны треугольника приблизительно равны 170 м. Волны двигались вправо (к берегу) со скоростью 0,2 м/с. Непрерывная линия показывает глубину изотермы (64 °Р), расположенной в термоклине (из [439]).

Вернуться к оглавлению