До сих пор рассматривались в основном детерминированные уравнения водного баланса для средних величин стока, осадков и испарения. Однако внешняя среда, действующая на такую глобальную природную систему, как Каспийское море, содержит значительные шумы, создаваемые флуктуациями климата, поэтому необходим вероятностный подход к описанию системы. Возникает проблема взаимодействия внутренней нелинейной динамики водного баланса и внешнего шума среды.[ ...]
В качестве индикаторов, сигнализирующих о качественных переходах в стохастических системах, будем рассматривать в соответствии с [Хорстхемке, Лефевр, 1987] экстремумы стационарной плотности вероятности уровня. Максимумы плотности вероятности отражают состояния, в которых море находится относительно продолжительное время, а минимумы плотности вероятности - состояния, в которых море находится недолго.[ ...]
Положим, что сток и скорость видимого испарения - случайные процессы Орнштейна-Уленбека (это предположение можно существенно ослабить и рассматривать марковские процессы с сильным "перемешиванием"), кроме того, примем, что слой испарения (при учете взаимодействия залива Кара-Богаз-Гол и Каспийского моря к этой величине необходимо добавить слой стока в залив как функцию уровня) содержит тепловую компоненту, которая зависит от уровня моря.[ ...]
Шум слоя испарения не влияет на положение экстремумов, так как является аддитивной величиной, которая не зависит от уровня моря.[ ...]
Далее рассмотрим применение известных математических методов [Хорстхемке, Лефевр, 1987; Гардинер, 1986] для описания многолетних колебаний уровня водоемов.[ ...]
Реально приток речных вод <2 и слой испарения Е испытывают сильные колебания во времени, которые порождены климатическими флуктуациями на водосборе. Например, среднеквадратическое отклонение стока Волги равно 50 км3/год, что составляет -20% среднего значения стока.[ ...]
Здесь р(у, t/x, s) - плотность вероятности перехода марковского процесса X, (х его значение в момент времени s, у - в момент времени t).[ ...]
Прилагательное "обратное" входит в название этого уравнения потому, что вариация берется как бы относительно начального состояния х и начального момента времени s. Конечное состояние (у, t) входит в решение обратного уравнения Колмогорова как параметр. Можно сказать, что это уравнение дает решение задачи, в которой процесс X, должен начаться в момент времени s, чтобы в момент t перейти в заданное состояние у. Это уравнение будет использовано нами при определении случайной величины - времени перехода водоема из одного состояния в другое.[ ...]
Проанализируем это уравнение [Хорстхемке, Лефевр, 1987]. Рассмотрим интерпретацию Ито.[ ...]
Рисунки к данной главе:
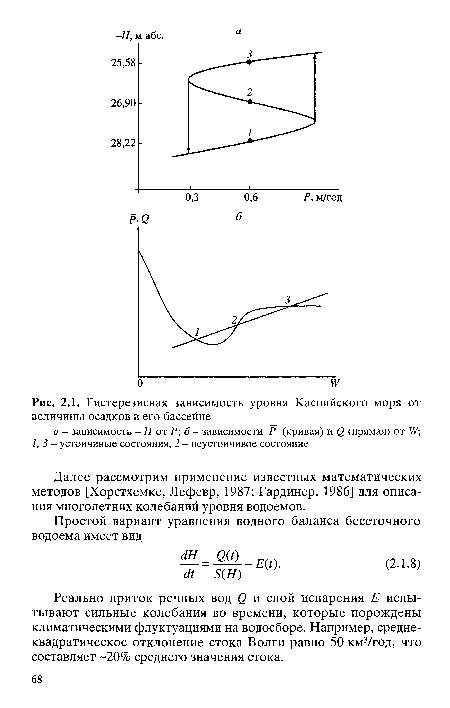
| Гистерезисная зависимость уровня Каспийского моря от величины осадков в его бассейне |
 |
Аналогичные главы в дргуих документах:
| См. далее:Постановка задачи |
| См. далее:Постановка задачи |
| См. далее:Постановка задачи |
| См. далее:Постановка задачи |