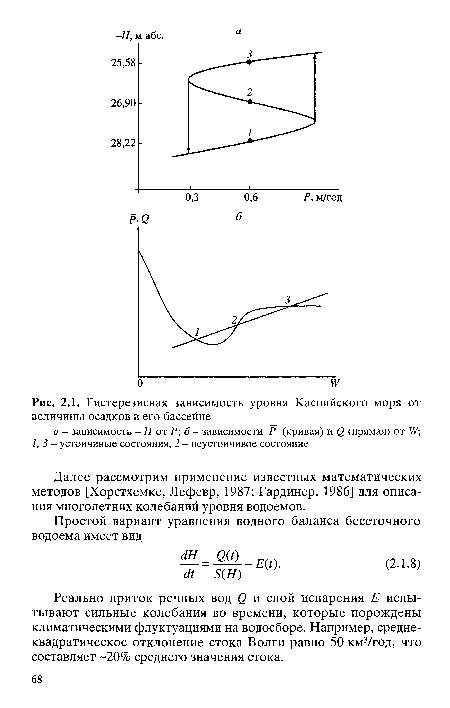
Так как для Каспия 5 (Я) > 0, то наиболее вероятные уровни лежат выше равновесных, и шум стока способствует сдвигу детерминированной бифуркационной диаграммы. Правая часть уравнения (2.1.7) обычно очень мала, поэтому можно принять, что 1№(Н Э) = Щ, Н э = Я,, г = 1,2,3, т.е. в этом приближении наиболее вероятные моды совпадают с равновесными уровнями (рис. 2.1). Точки пересечения зависимостей эффективных осадков (физические осадки минус испарение) и стока от увлажненности бассейна (точки 1, 2, 3) соответствуют равновесным значениям увлажненности и уровня. Таким образом, распределение плотности вероятностей уровней Каспийского моря не является гауссовым. Это распределение с двумя максимумами, расположенными при Я = Яь Я = Я3, разделенными точкой минимума при Я = Я2 (неустойчивый уровень). Равновесное состояние моря, представленное пиком при Я = Я,, является метастабильным (долгоживущим) и его вероятность медленно убывает в пользу пика при Я = Я3. Как было показано выше, достаточно длительное превышение норм поступления стока или выпадения осадков может перевести море с уровня Н} на уровень Я3. Грубой мерой вероятности такого события является высота потенциального барьера, разделяющего равновесные уровни, а время перехода определяется расстоянием между уровнями.~~Обработка данных наблюдений показала, что при одном и том же количестве осадков в бассейне моря при современном климате существуют два устойчивых равновесных значения () (320 и 270 км3/год) и соответственно два значения Я (-25,47 и -27,92 м абс.) (см. рис. 2.1). В нижней части рисунка приведены зависимости величин эффективных осадков (осадки минус испарение) и речного стока от влагозапасов; точки 1, 2, 3 являются решениями уравнения водного баланса бассейна моря. Подчеркнем, что бимодальность распределения стационарной плотности уровня моря объясняется водными процессами на водосборе, а не зависимостью слоя испарения с поверхности моря от уровня. По существу, система нелинейных уравнений (2.2.1) связывает колебания уровня Каспийского моря с изменениями климата его бассейна. Известно, что случайный процесс, характеризуемый бимодальным распределением плотности вероятности - смесь двух гауссовых случайных процессов (каждый из этих процессов порождается небольшими колебаниями Я вблизи одного из устойчивых состояний равновесия), поэтому временной ряд многолетних колебаний стока Волги должен быть нестационарным и неоднородным. Детальный анализ статистических характеристик годового стока Волги у Волгограда подтвердил приведенный выше анализ [Исмайылов, Федоров, 2001].
Вернуться к оглавлению