При развитии методов прогноза загрязнения воздуха существенное значение приобретает исключение из исходной информации и исследуемых процессов случайных эффектов. Это связано не только с необходимостью учета большого числа недостаточно определенных факторов, но и с тем, что часть из них (например, трансформация примесей, взаимодействие примесей с подстилающей поверхностью и т. п.) нередко совсем не принимаются во внимание. Всегда имеются и случайные погрешности измерений. В прогнозируемых величинах вследствие указанных эффектов создается некий случайный фон или «шум». Фильтрация (исключение) шумов должна, естественно, повысить достоверность и оправ-дываемость прогнозов. В целях такой фильтрации при рассмотрении случайных процессов в современном статистическом анализе, в частности в исследованиях по автоматическим системам контроля, развит ряд приемов. Некоторые из них были доложены на Международном симпозиуме в Киото (Япония), состоявшемся в 1977 г. и на совещании в Международном институте по системному анализу в Лаксенбурге (Австрия) в 1979 г.[ ...]
Если обозначить через А коэффициент ослабления (на нулевой частоте) для фильтра третьего порядка, а сам этот фильтр представить в виде суперпозиции трех фильтров первого порядка с постоянными времени s , S2 и s3, то при времени прогноза td процедура вычислений будет состоять из следующих четырех шагов.[ ...]
Некоторые результаты моделирования на ЭВМ случайного процесса изменения концентрации примеси, основанного на применении фильтра третьего порядка и прогноза этого процесса с использованием различных фильтров, представлены графически. Во всех случаях заблаговременность соответствовала предсказуемости 0,9 или выше, т. е. выбиралось ¿сг = £5//4 или ¿¿ = 2 5,-/5, а постоянные времени принимались: 51 = 16, 52 = 20, 5з = 25. Из-сопоставления модельного процесса и результатов его прогноза с помощью винеровского фильтра при ¿¿=10 и ¿¿=15 видно, как меняется качество прогноза при уменьшении предсказуемости от 0,95 до 0,9.[ ...]
Поскольку Кокю анализировал ситуацию, когда прогноз загрязнения воздуха дается без использования добавочной метеорологической информации, его результат характеризует максимум возможного, что можно получить с использованием только внутренней связности процесса изменения загрязнения воздуха.[ ...]
Для реальных флуктуаций концентрации примеси в течение суток в городе, согласно приведенным в п. 4.1 данным Зайцева (1973), характерные времена составляют 3 мин, 20 мни и 8 ч (см. рис. 4.7). Поскольку различие между этими временами весьма велико, то предсказуемость г2 = 0,8 должна соответствовать значению =—2 Я/, так что /¿ = 2 ч — верхний предел заблаговременности для таких прогностических схем.[ ...]
Уравнение (4.23), сходное с (4.4), использовано в той же работе Соеда при изложении метода множественной регрессии. Отличие уравнения (4.23) состоит в том, что в него введены добавочные члены u(k—1) и v(k) — n-мерные независимые векторы «шума» с нулевым средним, т. е. «белого шума», характеризуемые ковариационными матрицами соответственно Q (k) п R(k).[ ...]
Одновременно оценивалась погрешность инерционного прогноза, когда сохранялись исходные значения прогнозируемых величин. Для него оказалось / = 0,628. Полученные результаты для случая использования различных предикторов даны в табл. 4.10, из которой следует, что примененне фильтра Калмана ведет к уменьшению погрешности по сравнению с инерционным прогнозом почти в два раза.[ ...]
Наибольшая прогностическая точность достигается при использовании в качестве предиктора только О . Увеличение количества регистрируемых примесей, как видно, не всегда приводит к улучшению результатов прогноза.[ ...]
Сопоставление полученных погрешностей с результатами прогноза по более простым статистическим моделям, в частности, указанным в п. 4.2, позволяет сделать вывод, что введение фильтра Калмана повышает точность прогноза.[ ...]
Рисунки к данной главе:
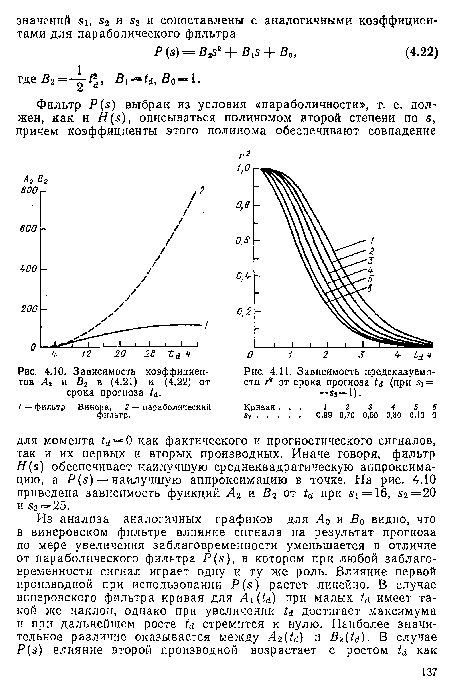
| Зависимость предсказуемости г2 от срока прогноза t<t (при si = =s3=l). |
 |