Уравнения (4) и (7) применимы к обеим фазам, но ниже символы без штрихов будут относиться к жидкой фазе, прописные буквы используются для значений параметров на стенке пузырька, а штрихами будут отмечены символы, относящиеся к газопаровой фазе внутри пузырька.[ ...]
При таком равновесии диффузия газа из пузырька в жидкость не учитывается. Поэтому равновесие является лишь квазиста-ционарным.[ ...]
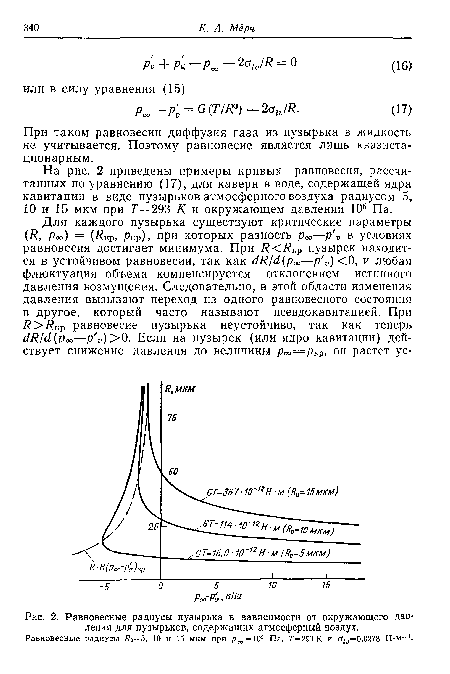
На рис. 2 приведены примеры кривых равновесия, рассчитанных по уравнению (17), для каверн в воде, содержащей ядра кавитации в виде пузырьков атмосферного воздуха радиусом 5, 10 и 15 мкм при 7 = 293 К и окружающем давлении 105 Па.[ ...]
Равновесные радиусы Яо=5, 10 и 15 мкм при Роо = 105 Па, Т=293 К и сг/о=0,0278 Н-м- .[ ...]
Значения G для разных ядер кавитации различны, и поэтому различаются и значения рЩ). Следовательно, при заданном минимальном окружающем давлении спектр размеров ядер является определяющим при решении вопроса о том, какие ядра останутся только ядрами, а какие разовьются в большие пузыри и где возникнет кавитация. При сравнении результатов экспериментов по кавитации необходимо учитывать спектр ядер кавитации. Это является одной из проблем моделирования, рассматриваемого в разд. 8.[ ...]
Когда пузырьки, образовавшиеся в результате паровой кавитации, подвергаются действию давления, превышающего давление насыщенного пара р и, они начинают схлопываться.[ ...]
Согласно этому решению, скорость схлопывания стремится к бесконечности, когда Я—>-0, но при этом уравнение (21) становится непригодным. Каверну нельзя считать пустой на конечных стадиях схлопывания, когда нужно учитывать, во-первых, тепловые эффекты и, во-вторых, сжимаемость жидкости. При больших скоростях движения стенки на конечных стадиях схлопывания выделение теплоты конденсации увеличивает температуру газопарового содержимого каверны. Когда конденсация не может поддерживаться на уровне, соответствующем скорости стенки [51], часть пара сжимается вместе с неконденсируемым газом, что приводит к дальнейшему нагреванию, и в конце концов внутри схлопывающейся каверны возникают очень высокие давления.[ ...]
Эти результаты дают очень хорошее приближение для действительных времен схлопывания, за исключением жидкостей, обладающих очень большой вязкостью (разд. 3.2.2). Непригодность теории несжимаемой жидкости при определении движения стенки на конечной стадии схлопывания почти не имеет значения для вычисления времени схлопывания, так как длительность этой конечной стадии крайне мала. Отклонения окружающего давления рос от постоянной величины могут приводить к расхождению экспериментальных и расчетных величин; на время схлопывания оказывает сильное влияние также несферич-ность схлопывания, хотя даже в этом случае различия не слишком велики (разд. 3.3).[ ...]
Если жидкость несжимаемая и невязкая, то при сжатии каверны эта энергия превращается в кинетическую энергию Екнн Я/? сю (/?ао—Я3), и возникает поле скоростей, описываемое уравнениями (12) и (22). Скорость стенки каверны, соответствующая теории Рэлея для несжимаемой жидкости, приведена, на рис. 6 (пустая каверна). Видно, что при Я—Я) скорость стремится к бесконечности пропорционально (/?о/ )1;5, но при фиксированных значениях г скорость и—>-0. Таким образом, при Н— 0 кинетическая энергия, существовавшая вначале в форме потенциальной энергии жидкости, сосредоточивается в очень тонком слое жидкости малого объема, примыкающем к стенке каверны. Чтобы избежать получения явно ошибочного результата, состоящего в стремлении скорости стенки пузырька к бесконечности, Рэлей рассмотрел схлопывание каверны, содержащей газ, который сжимается изотермически. Это приводит к появлению конечных скоростей схлопывания и минимального размера пузырька, и, если не учитывать диссипацию, обусловленную тепловыми, вязкими и акустическими эффектами, каверна пульсирует, принимая попеременно, начальный и минимальный размеры. Хотя в действительности диссипация играет важную роль, этот процесс иллюстрирует, как сжатие газа приводит к повторному образованию пузырька после схлопывания.[ ...]
Критическую величину числа Рейнольдса нашел Забабахин [72], и найденное им значение Некр = 8,4 очень хорошо согласуется со значением г) — 0,46. При Не Некр влиянием вязкости можно пренебречь.[ ...]
Рисунки к данной главе:
| Равновесные радиусы пузырька в зависимости от окружающего давления для пузырьков, содержащих атмосферный воздух. |
 |
| Распределение давления в жидкости при различных положениях стенки пузырька во время схлопывания сферической каверны, вычисленное по теории Рэлея для несжимаемой жидкости (уравнение (26));!, |
 |
| Число Маха стенки пузырька в зависимости от его радиуса при уменьшении содержания газа [24]. |
![Число Маха стенки пузырька в зависимости от его радиуса при уменьшении содержания газа [24].](/static/pngsmall/950005602.png) |
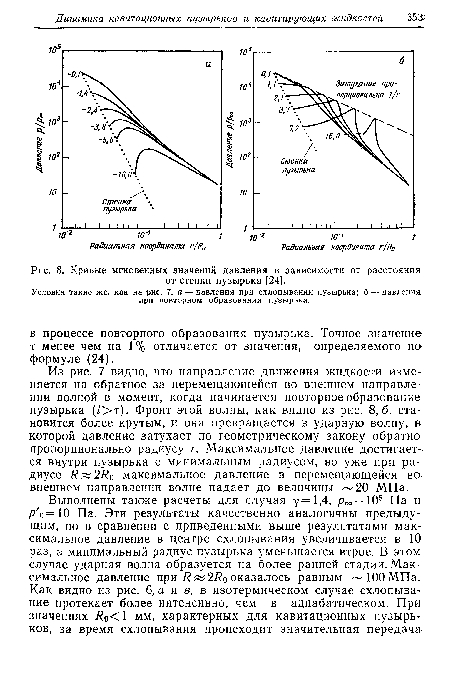
| Кривые мгновенных значений давления в зависимости от расстояния |
 |
| Формы поверхности пузырька для случая b/R0= 1 [53]. (С разрешения Cambridge University Press.) |
![Формы поверхности пузырька для случая b/R0= 1 [53]. (С разрешения Cambridge University Press.)](/static/pngsmall/950005620.png) |
| Формы поверхности пузырька для случая b/R0= 1,5 [53]. (С разрешения Cambridge University Press.) |
![Формы поверхности пузырька для случая b/R0= 1,5 [53]. (С разрешения Cambridge University Press.)](/static/pngsmall/950005620.png) |
![Кривые мгновенных значений числа Маха в зависимости от расстояния от стенки пузырька в процессе его схлопывания и повторного образования [24]. Начальное внутреннее давление газа р о—102 Па, давление окружающей среды Па,](/static/pngsmall/950005608.png)