Поля динамических напряжений и характеристики разрушения слишком сложны, чтобы можно было разработать аналитические модели, дающие полное количественное описание ударного разрушения. Наиболее разумный подход при создании моделей ударного разрушения заключается в принятии некоторых постулатов, которые описывают наиболее существенные стороны явления, с последующей проверкой и уточнением их с помощью отдельных численных расчетов. В результате такого подхода появляются безразмерные функции, связывающие основные характеристики материалов и параметры удара. Эти функции можно использовать для корреляции экспериментальных данных по ударному разрушению и, следовательно, для подтверждения принятых постулатов и получения численных значений коэффициентов. Этот подход только еще складывается, и пока можно описать лишь предварительные результаты. Тем не менее подробное его описание полезно и будет приведено ниже. Сначала обсудим численные методы, поскольку они одинаковы для всех механизмов разрушения, а затем рассмотрим модели, пригодные для описания конкретных механизмов разрушения.[ ...]
Программы расчета распространения трещин еще находятся в стадии разработки, однако предварительные расчеты [42] подтвердили, что для устойчивого роста трещин (независимо от выбора сетки) должны выполняться условия для напряжений в вершине трещины типа уравнения (27).[ ...]
Если отказаться от квазистатического подхода и рассматривать динамическую задачу, то придется вводить аналогичные параметры контакта, которые определяют максимальное напряжение растяжения и протяженность упругой зоны. Эти допущения могут быть трех типов: растрескивание определяется остаточными напряжениями (как в квазистатической задаче) [10], условиями контакта при максимальном проникании и условиями контакта на начальной стадии удара. Рассмотрим следствия этих допущений на основе данных, приведенных в табл. 1.[ ...]
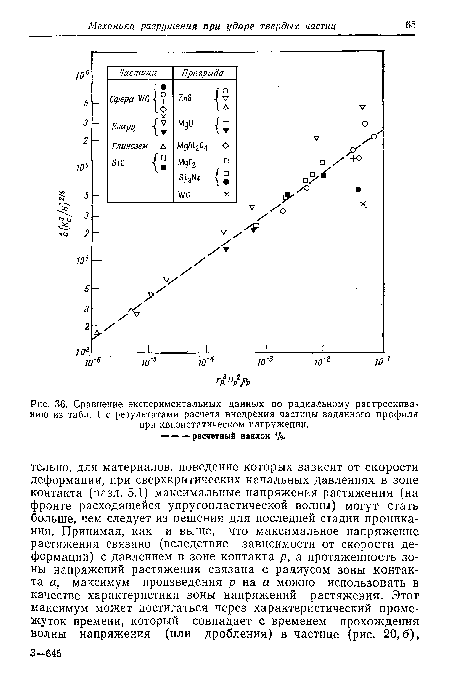
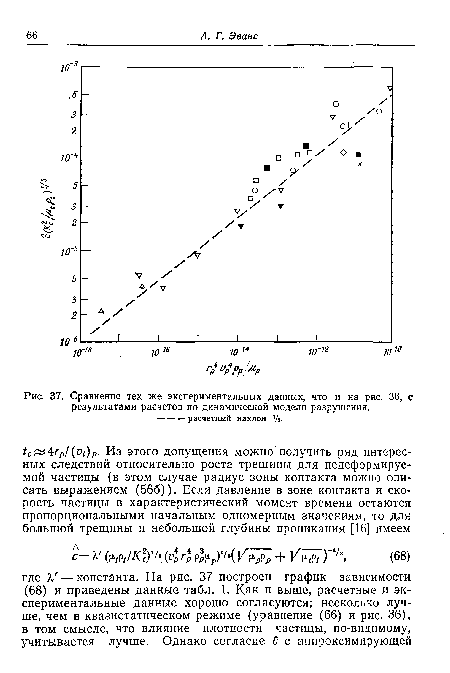
Здесь содержится неявное предположение, что влияние временных эффектов на рост трещины, обсуждавшееся в разд. 3.2, несущественно, так что волновые свойства преграды можно не учитывать. Некоторым основанием для пренебрежения временными эффектами может явиться то обстоятельство, что распространение зоны напряжений растяжения, которое вблизи максимума напряжения зависит от скорости распространения сравнительно медленно движущейся упругопластической волны, вполне может происходить со скоростью, меньшей скорости роста трещины (максимальная величина которой равна скорости волны Рэлея). На рис. 36 построен график зависимости (66) и там же приведены данные табл. 1. Как видно из рисунка, согласие теоретических и экспериментальных результатов вполне удовлетворительное. Единственное значительное различие связано с влиянием плотности частицы и преграды в том смысле, что при больших значениях их плотности ( УС) длина трещины во всех случаях меньше расчетной.[ ...]
Это уравнение дает практически те же результаты, что и уравнение (66) для материалов, перечисленных в табл. 1, так как твердость и модуль сдвига у этих материалов приблизительно пропорциональны. Какое из этих решений лучше, можно установить только путем экспериментов с материалами, у которых Н и ¡и? существенно не пропорциональны.[ ...]
Таким образом радиальное растрескивание достаточно хорошо описывается соотношениями, полученными на основании нескольких существенно различающихся допущений для больших (по сравнению с радиусом зоны контакта) трещин, а именно допущений о квазистатическом нагружении жесткопластичного или упругого материала и динамическом нагружении. Последнее допущение является наиболее подходящим, однако нужны дальнейшие исследования для того, чтобы выяснить, почему при столь разных допущениях получаются близкие результаты, а также для того, чтобы разработать более сложные модели, необходимые для проведения более точных расчетов роста трещины.[ ...]
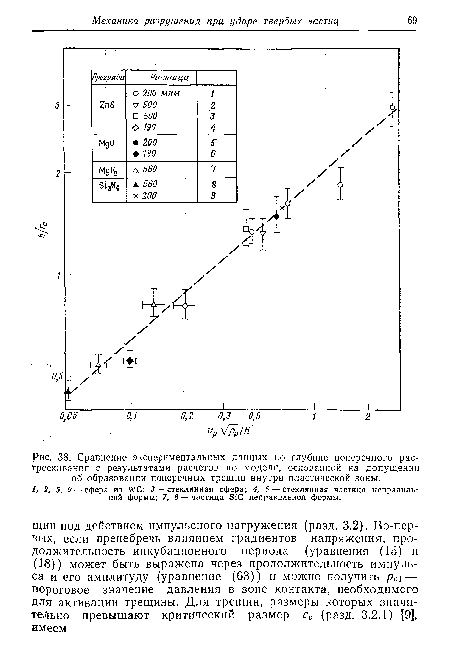
Согласие расчетов с экспериментальными данными из табл. 2 достаточно хорошее (рис. 38), что до некоторой степени подтверждает принятую модель. Однако этот анализ следует рассматривать как предварительный, и необходимо проведение серьезных дополнительных исследований, прежде чем будет создана достаточно точная модель поперечного растрескивания.[ ...]
Некоторые важные закономерности для порога разрушения в зависимости от свойств преграды изучались экспериментально. В частности, изучалось влияние трещиностойкости и скорости распространения волны [9]. На важную роль Кс и VI указывают уравнения (77) и (79), которые качественно согласуются с экспериментальными данными (табл. 3). Однако неопределенность, связанная с размером исходных микротрещин, не позволяет провести количественное сравнение. Этот вопрос требует дальнейшего изучения. Экспериментальные данные о послепо-роговом росте трещины (уравнение (79)) отсутствуют, главным образом из-за того, что при каждом ударе возникают многочисленные разрушения. По этой же причине количественно не изучалась очень сложная картина, которая наблюдается на предварительно поврежденных поверхностях.[ ...]
Таким образом, существующий уровень понимания механизмов разрушения почти достаточен для выбора и разработки материалов. Недостаточность наших знаний проявляется только при попытке подробного описания типа и масштаба разрушения для данной комбинации частица — преграда. Для удовлетворительного выполнения этой задачи необходимы дополнительные исследования.[ ...]
Рисунки к данной главе:
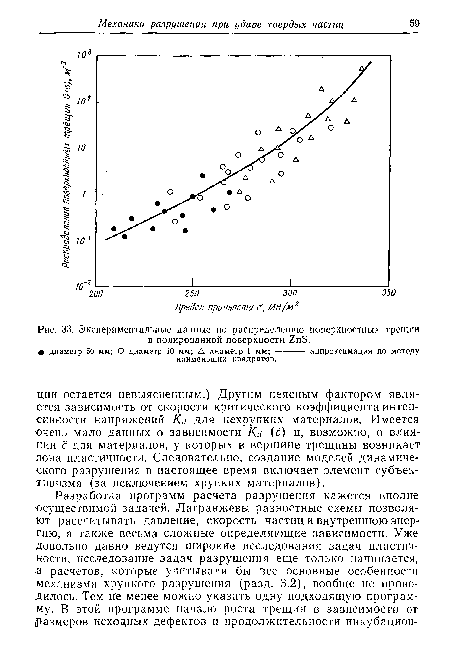
| Экспериментальные данные по распределению поверхностных трещин в полированной поверхности 2пБ. |
 |
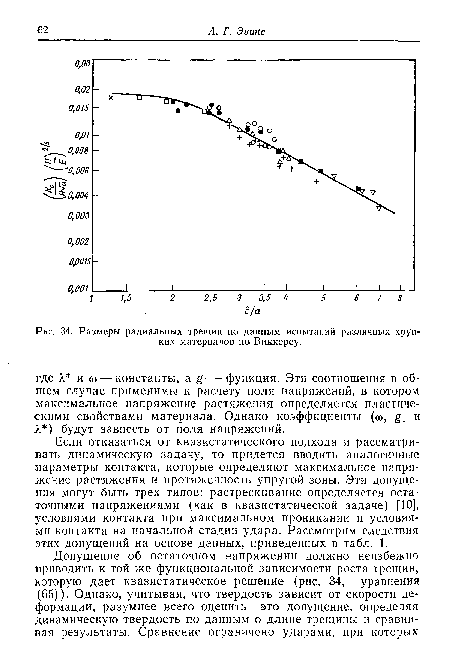
| Размеры радиальных трещин по данным испытаний различных хрупких материалов по Виккерсу. |
 |
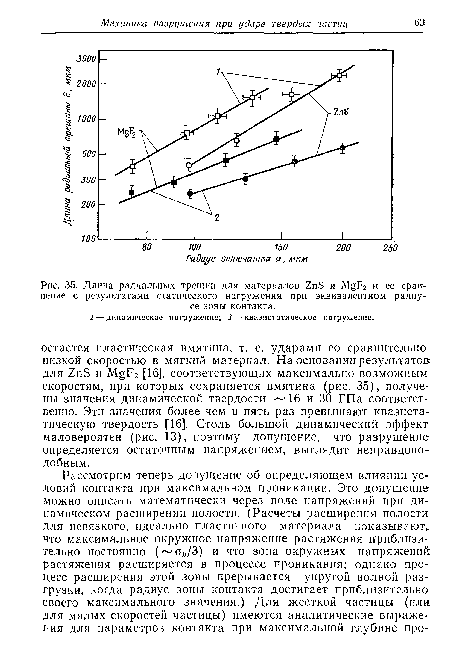
| Длина радиальных трещин для материалов 2пБ и М§Р2 и ее сравнение с результатами статического нагружения при эквивалентном радиусе зоны контакта. |
 |
| Сравнение экспериментальных данных по радиальному растрескиванию из табл. I с результатами расчета внедрения частицы заданного профиля при квазистатическом нагружении. |
 |
| Сравнение тех же экспериментальных данных, что и на рис. 36, с результатами расчетов по динамической модели разрушения. |
 |
| Сравнение экспериментальных данных по глубине поперечного растрескивания с результатами расчетов по модели, основанной на допущении об образовании поперечных трещин внутри пластической зоны. |
 |
| Рост трещины в квазистатическом, экспоненциально изменяющемся |
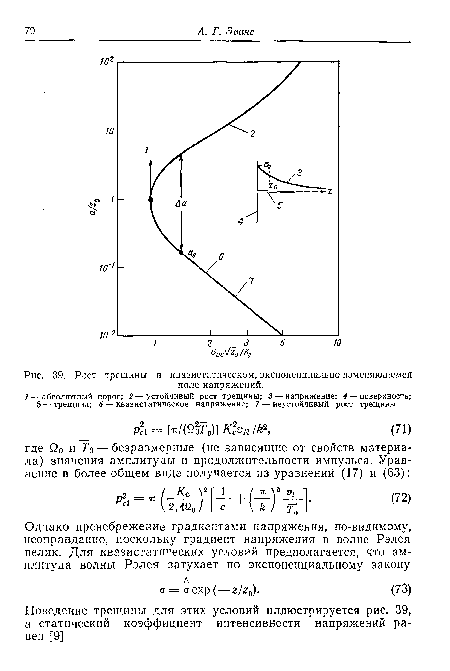 |