Получив дифференциальное уравнение термобарических волн в форме (223), мы вынуждены были лишь предварительно проанализировать физический смысл искажающих членов ф (¿) и гр (х, у, ¿). Первый из них от брасывается совершенно безболезненно, а второй по существу влияет на ха рактер колебаний: он показывает, что пучности и узловые линии в поле термобарических сейш обязаны вращаться благодаря наличию кориолисовой силы и что амплитуда колебаний должна изменяться во времени (мы описали это изменение экспоненциальной функцией времени для суждения о его порядке).[ ...]
Несовершенство современного математического аппарата не позволило ни Шулейкину, ни последующим авторам найти полный интеграл уравнения (223), а потому пришлось возвратиться к грубо упрощенной форме (229), допускающей интегрирование в конкретных граничных условиях применительно к узловой линии в форме окружности.[ ...]
Попытаемся теперь поправить теоретические выводы, исходя из действительной картины явления, запечатленной на кадрах Сандстрема. Вообразим прежде всего те изменения температурного поля рис. 369, которые должны происходить во времени согласно грубо приближенному уравнению (229).[ ...]
Очевидно, также по формуле (232) следует ожидать, что во время вращения всей сетки все изоплеты сохранят взаимное положение (одна относительно другой) и при каждой из них сохранится та же самая цифра, какая отмечала значение температурного отклонения в начальной фазе на рис. 369.[ ...]
В действительности картина сейш несколько иная. Прежде всего кадры Сандстрема явно «обесцвечиваются» при переходе от двух крайних фаз, изображенных на рис. 370 и 371, к фазам промежуточным. Особенно бледная картина получается при повороте системы примерно на прямой угол, как видно на рис. 375, где повторены соответствующие «кадры» цветной вкладки. Вместо отклонения температуры в пучностях на 6 или 5° от климатологической нормы, как это было в крайних фазах, здесь можно отметить лишь отклонения от нормы на 2 или даже на 1°.[ ...]
На рис. 376 изображено расположение этих точек относительно рамки сандстремовских кадров. Значение векторов, нанесенных на том же рисунке, будет пояснено ниже. Отметив такие точки на восковой бумаге и налагая их последовательно на кадры, легко было затем построить диаграмму, показывающую, как меняется во времени температурное отклонение в той или иной из выбранных восьми точек. Сводная диаграмма, содержащая все восемь кривых, воспроизведена на рис. 377. Буква, проставленная при каждой кривой, показывает, какой именно точке соответствует данная кривая.[ ...]
Гармонический анализ кривых был проделан посредством анализатора Мадер — Отта. Результаты сведены в табл. 19.[ ...]
Высшие гармонические дают еще меньшие значения коэффициентов а и Ъ в ряде Фурье.[ ...]
В табл. 19 через а0 обозначен постоянный член ряда Фурье, буквами а с соответствующими индексами — коэффициенты при косинусах, а буквами Ь — при синусах в том же ряде.[ ...]
Переходим теперь к выводам из гармонического анализа. Заметим, что наиболее надежным элементом основных колебаний придется признать фазу: ведь амплитуда этих колебаний должна чрезвычайно резко меняться в зависимости от значения радиус-вектора, а последнее значение не поддается точному измерению ввиду некоторой неопределенности контура, выделенного на рис. 376; значительно меньшая ошибка возможна при определении углов г ). Вот почему мы ограничимся здесь лишь учетом фазовых углов, которые получаются в результате сопоставления а1 и Ъ1 для восьми выбранных точек. В табл. 20 выписаны эти углы.[ ...]
Рисунки к данной главе:
| Промежуточные фазы колебаний в серии Сандстрема |
 |
| Выбор точек для анализа колебаний |
 |
| Кривые колебаний в восьми точках поля |
 |
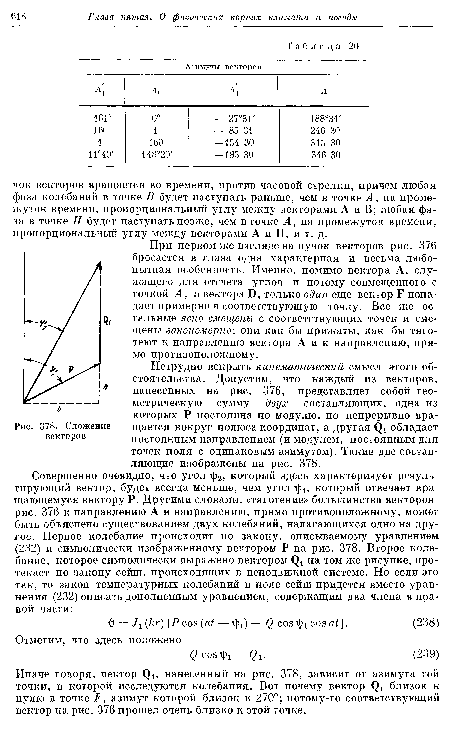
| Сложение векторов |
 |
| Сложное температурное поле в различных фазах колебаний |
 |