Как мы видели в предыдущем параграфе, даже параболическая форма береговой линии создает большие трудности для расчета напряженности муссонного поля против мыса, или полуострова, и задача приводится к суммированию рядов, которые сходятся очень медленно. Тем более при произвольной форме береговой линии казалось бы должны возникать трудности подобного расчета, к преодолению которых нет пути.[ ...]
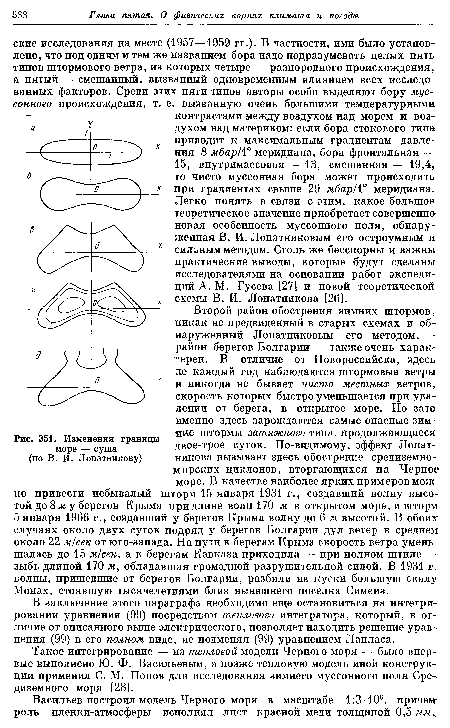
Но автор работы не ограничивается таким приближением, а идет дальше. Прежде всего он сглаживает юго-западный и юго-восточный углы кривой, внося в уравнение дополнительную функцию от х и у. Тогда береговая линия приобретает форму, изображенную на рис. 351, г, где вычерчены и некоторые изаномалы температуры воздуха над морем.[ ...]
Аналитические выражения поля изаномал позволяют В. И. Лопатникову найти градиенты температурной аномалии в различных наиболее интересных точках береговой линии. Замечательно, что обострение муссонного поля обнаруживается не только там, где его можно было ожидать на основании соображений, изложенных в предыдущих параграфах,— не только против остроконечных мысов, но и на участках береговой линии, протянувшихся спокойно,— несколько южней Новороссийска и затем вблизи от устья р. Дунай.[ ...]
Дальнейшая детализация картины поля была проведена путем разрыва береговой линии по схеме рис. 351, д и аналогичного разрыва в юго-западном углу кривой. Тем самым моделировалось влияние Днепровского лимана, Азовского моря и, с другой стороны, Мраморного моря с Босфором. Оказалось при этом, что местные максимумы градиентов температурной аномалии, а стало быть и градиентов давления, на основании (68), смещаются: один из них, очень резкий, приходится в точности на Новороссийск, а другой — на район между Варной и Бургасом. В первом из этих районов ежегодно наблюдается бора — ветер, достигающий скоростей более 40 м/сек.[ ...]
В заключение этого параграфа необходимо еще остановиться на интегрировании уравнения (99) посредством теплового интегратора, который, в отличие от описанного выше электрического, позволяет находить решение уравнения (99) в его полном виде, не подменяя (99) уравнением Лапласа.[ ...]
Такое интегрирование — на тепловой модели Черного моря — было впервые выполнено Ю. Ф. Васильевым, а позже тепловую модель иной конструкции применил С. М. Попов для исследования зимнего муссонного поля Средиземного моря [28].[ ...]
Васильев построил модель Черного моря в масштабе 1:3- 10е, причем роль пленки-атмосферы исполнял лист красной меди толщиной 0,5 мм,.[ ...]
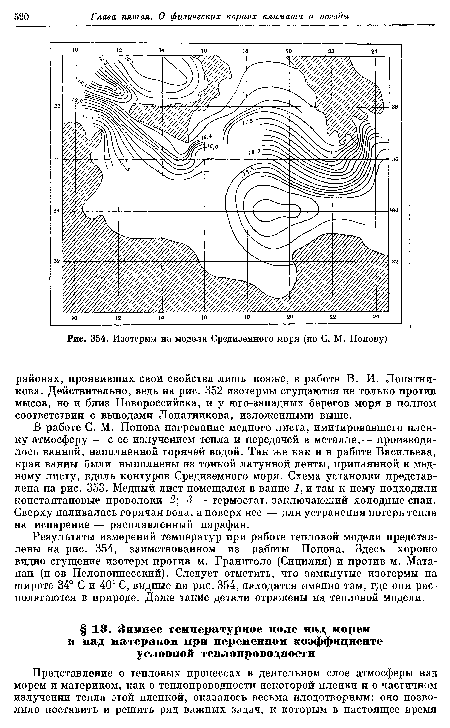
В работе С. М. Попова нагревание медного листа, имитировавшего пленку-атмосферу — с ее излучением тепла и передачей в металле,— производилось ванной, наполненной горячей водой. Так же как и в работе Васильева, края ванны были выполнены из тонкой латунной ленты, припаянной к медному листу, вдоль контуров Средиземного моря. Схема установки представлена на рис. 353. Медный лист помещался в ванне 1, и там к нему подходили константановые проволоки 2,3 — термостат, заключающий холодные спаи. Сверху наливалась горячая вода, а поверх нее — для устранения потерь тепла на испарение — расплавленный парафин.[ ...]
Результаты измерений температур при работе тепловой модели представлены на рис. 354, заимствованном из работы Попова. Здесь хорошо видно сгущение изотерм против м. Гранитоло (Сицилия) и против м. Мата-пан (п-ов Пелопоннесский). Следует отметить, что замкнутые изотермы на широте 34° С и 40° С, видные на рис. 354, находятся именно там, где они располагаются в природе. Даже такие детали отражены на тепловой модели.[ ...]
Рисунки к данной главе:
| Изменения границы море — суша (по В. И. Лопатникову) |
 |
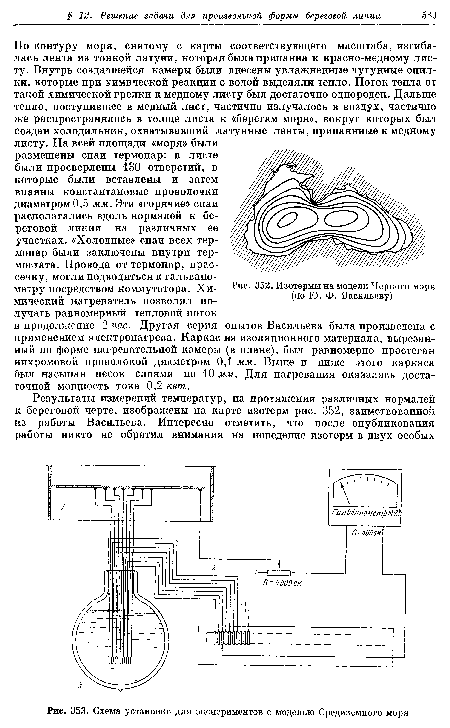
| Изотермы на модели Черного моря (по Ю. Ф. Васильеву) |
 |
| Схема установки для экспериментов с моделью Средиземного моря |
 |
| Изотермы на модели Средиземного моря (по С. М. Попову) |
 |