Приближенное решение, приведенное в предыдущем параграфе, дало результаты, удовлетворительно оправдывающиеся в природе с качественной стороны. Для суждения о стороне количественной весьма важно попытаться решить задачу более точным методом, хотя бы для ограниченного числа случаев, и сопоставить между собой результаты приближенного и более точного решений.[ ...]
Такое уточнение решения было произведено Я. И. Секерж-Зеньковичем 24] применительно к двум частным случаям: случаю эллиптического острова и случаю параболического мыса. Воспроизведем здесь основные этапы его работы.[ ...]
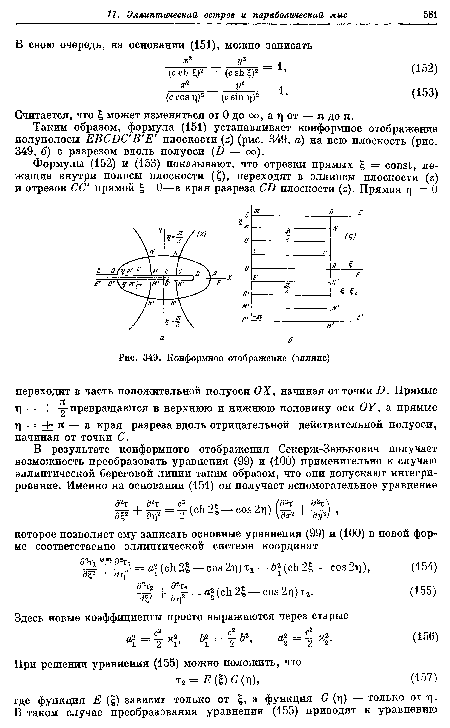
Считается, что £ может изменяться от 0 до оо, a rj от — я доя.[ ...]
Таким образом, формула (151) устанавливает конформное отображение полуполосы EBCDC B E плоскости (z) (рис. 349, а) на всю плоскость (рис. 349, б) с разрезом вдоль полуоси (D — оо).[ ...]
Не будем а смешивать с нашим параметром а .[ ...]
Эта формула описывает температурное поле над эллиптическим островом. Таким же путем Секерж-Зенькович, исходя из уравнения (154), определил и температурное поле над океаном, простирающимся вокруг острова.[ ...]
Предполагается, что г) может меняться от 0 до оо, а £ от — оо до оо. Тогда формула (168) устанавливает конформное отображение верхней полуплоскости плоскости (z) (рис. 350, а) на всю плоскость (Q (рис. 350, б) с разрезом вдоль действительной полуоси ОХ. На обоих рисунках точки и их отображения обозначены одинаковыми буквами.[ ...]
На основании (170) и (171) полупрямые £ = ± С = const при г О переходят в верхнюю и в нижнюю половины парабол (170) с вершинами, лежащими на оси ОХ; их оси симметрии совпадают с отрицательной оськ> ОХ. Общий фокус всех этих парабол лежит в начале координат. Прямые Л == Ло const переходят в параболы (171), ортогональные к параболам (170) и конфокальные с ними. В отличие от первых парабол, оси симметрии теперь направлены в сторону положительной оси ОХ.[ ...]
Аналогичные выражения получаются для поля над морем.[ ...]
К сожалению, в результате получаются ряды, которые очень медленно сходятся. Поэтому вычисление напряженности поля против параболического полуострова, мыса или залива производится со значительно меньшей надежностью, чем это удалось сделать Секерж-Зеньковичу применительно к берегам эллиптического моря или эллиптического острова. Задаваясь параболической береговой линией с радиусом кривизны у вершины, равным 250 км, и полагая, что температурная аномалия на берегу равна 3°, он получает для температурного градиента у самой вершины параболы значение 0,0164 град!км.[ ...]
Рисунки к данной главе:
| Конформное отображение (эллипс) |
 |
| Конформное отображение (парабола) |
 |