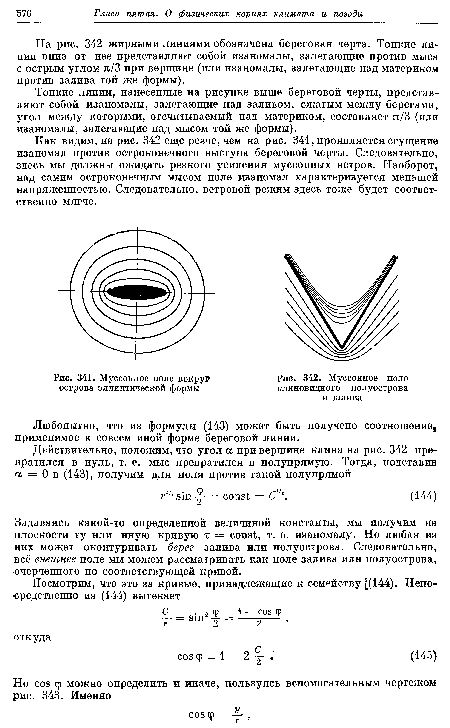
На рис. 341 изображена картина муссонного поля вокруг острова эллиптической формы (над морем) или вокруг моря подобной же формы (над материком). Обращает на себя внимание сгущение изаномал против вершин эллипса с наибольшей кривизной и разрежение их против тех участков, где кривизна оказывается наименьшей.[ ...]
Формула (136) позволяет определить, во сколько раз температурный градиент против вершины эллипса (т. е. градиент вдоль оси X) превышает наименьший градиент (вдоль оси У) у берегов.[ ...]
Другими словами, искомое отношение градиентов равно отношению полуосей эллипса: градиент против вершин эллипса во столько раз превышает наименьший градиент у пологого берега острова, во сколько раз большая ось эллипса превышает малую.[ ...]
Совершенно очевидно, что подобное различие обостряется сильней всего у самих берегов эллиптического моря. При удалении от них величина chx/shT должна постепенно приближаться к единице. Иными словами, на большом расстоянии от эллиптического моря его муссонное поле все меньше и меньше отличается от поля круглого моря.[ ...]
Положим теперь, что требуется охарактеризовать муссонное поле против остроконечного полуострова, имеющего форму прямолинейно очерченного клина. Пусть угол при вершине этого клина равняется а. В таком случае уместно будет припомнить вторую аналогичную задачу, решенную Максвеллом для двух заряженных полуплоскостей, сходящихся клином под углом а.[ ...]
На рис. 342 жирными линиями обозначена береговая черта. Тонкие линии вниз от нее представляют собой изаномалы, залегающие против мыса с острым углом я/3 при вершине (или изаномалы, залегающие над материком против залива той же формы).[ ...]
Тонкие линии, нанесенные на рисунке выше береговой черты, представляют собой изаномалы, залегающие над заливом, сжатым между берегами, угол между которыми, отсчитываемый над материком, составляет я/3 (или изаномалы, залегающие над мысом той же формы).[ ...]
Как видим, на рис. 342 еще резче, чем на рис. 341, проявляется сгущение изаномал против остроконечного выступа береговой черты. Следовательно, здесь мы должны ожидать резкого усиления муссонных ветров. Наоборот, над самим остроконечным мысом поле изаномал характеризуется меньшей напряженностью. Следовательно, ветровой режим здесь тоже будет соответственно мягче.[ ...]
Любопытно, что из формулы (143) может быть получено соотношение, применимое к совсем иной форме береговой линии.[ ...]
Задаваясь какой-то определенной величиной константы, мы получим на плоскости ту или иную кривую т = const, т. е. изаномалу. Но любая из них может оконтуривать берег залива или полуострова. Следовательно, всё внешнее поле мы можем рассматривать как поле залива или полуострова, очерченного по соответствующей кривой.[ ...]
Рисунки к данной главе:
| Муссонное поле вокруг острова эллиптической формы |
 |
| Муссонное поле клиновидного полуострова и залива |
 |
| Вспомогательное построение |
 |
| Изаномалы Индостана |
 |
| Электрический интегратор уравнения Лапласа |
 |
| Поле вокруг модели материка Южной Америки |
 |
| Изменения направлений ветра на травер- |
 |
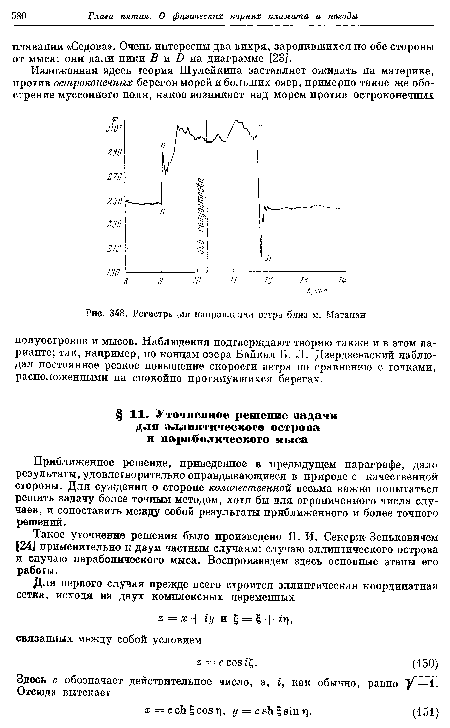
| Регистра направлений ветра близ м. Матапан |
 |