Особый принципиальный и практический интерес представляет задача о распространении температурных волн в толще морской воды при периодических изменениях температуры поверхностного слоя. Исследование этих волн позволяет определять К, а следовательно, и количество тепла, поступающего от одних слоев к другим.[ ...]
Как видим, колебания температуры на глубине 2 происходят с амплитудой 0O Z, уменьшающейся по экспоненциальному закону при возрастании z и со сдвигом фаз z по отношению к колебаниям поверхностной температуры; в свою очередь этот сдвиг фаз нарастает по линейному закону при увеличении 2. В формулу (29) входит период Т колебаний температуры, который таким образом оказывает решающее влияние на уменьшение амплитуды и на возрастание сдвига фаз.[ ...]
Большой интерес представляют задачи о выравнивании температур водных масс, связанные с интегрированием уравнения (26) применительно к заданным начальным условиям [17].[ ...]
В частном случае может оказаться, что в начальный момент времени соприкасаются между собой две водные массы, причем температура первой отлична от температуры второй на ДО.[ ...]
По оси ординат на рис. 257 отложены расстояния по вертикали от границы между двумя исследуемыми массами: вверх и вниз. Эти расстояния выражены в метрах. Кривые показывают распределение температур через 1,16; 11,6; 57,9 и 220 дней после начального момента —момента соприкосновения водных масс с разностью температур 5° между ними.[ ...]
Подобное же уравнение можно получить для самого общего случая переноса какой угодно величины. В частности, можно аналогичным путем исследовать изменение солености при вторжении более соленых вод в воды опресненные.[ ...]
Здесь С0 и Сп — постоянные, которые определяются на основании начальных условий (при х = 0.). Давая величине п, входящей в формулу (33), значения различных целых чисел, можно представить в виде ряда Фурье, все члены которого определяются на основании граничных условий.[ ...]
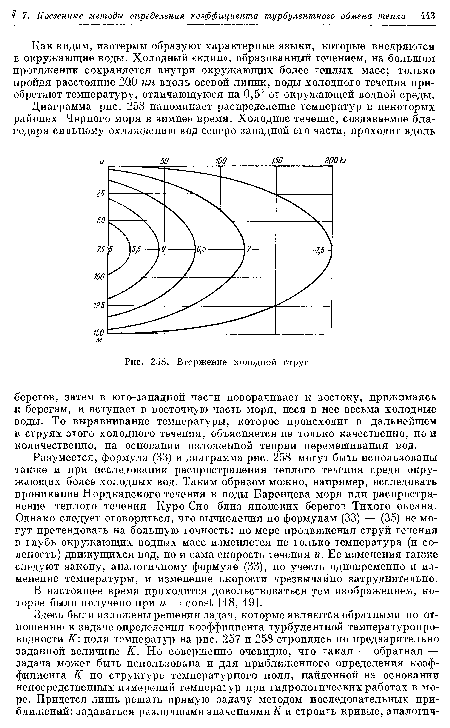
На рис. 258 графически представлены результаты вычисления по формуле (37). По оси абсцисс отложены расстояния от начальной плоскости, выраженные в километрах, а по оси ординат — глубины соответствующих горизонтов (полная глубина слоя, охваченного течением, равна 150. .м. Осевая линия проходит на глубине 75 м). Возле каждой изотермы, нанесенной на диаграмму, проставлено значение соответствующей температуры.[ ...]
Как видим, изотермы образуют характерные языки, которые внедряются в окружающие воды. Холодный «клин», образованный течением, на большом протяжении сохраняется внутри окружающих более теплых масс; только пройдя расстояние 200 км вдоль осевой линии, воды холодного течения приобретают температуру, отличающуюся на 0,5° от окружающей водной среды.[ ...]
Разумеется, формула (33) и диаграмма рис. 258 могут быть использованы также и при исследовании распространения теплого течения среди окружающих более холодных вод. Таким образом можно, например, исследовать проникание Нордкапского течения в воды Баренцева моря или распространение теплого течения Куро-Сио близ японских берегов Тихого океана. Однако следует оговориться, что вычисления по формулам (33) — (35) не могут претендовать на большую точность: по мере продвижения струй течения в глубь окружающих водных масс изменяется не только температура (и соленость) движущихся вод, но и сама скорость течения и. Ее изменения также следуют закону, аналогичному формуле (33), но учесть одновременно и изменение температуры, и изменение скорости чрезвычайно затруднительно.[ ...]
Рисунки к данной главе:
| Выравнивание температуры за различные сроки (по А. Дефанту) |
 |
| Вторжение холодной струи |
 |
| Изменения температур нию, он применим только в некоторых воды в Атлантическом океане частных случаях для определения обмена (по Гелланд-Гансену) масс промежуточного слоя с выше и ниже- |
 |
| Определение коэффициента перемешивания (по И. Фьелдстаду) |
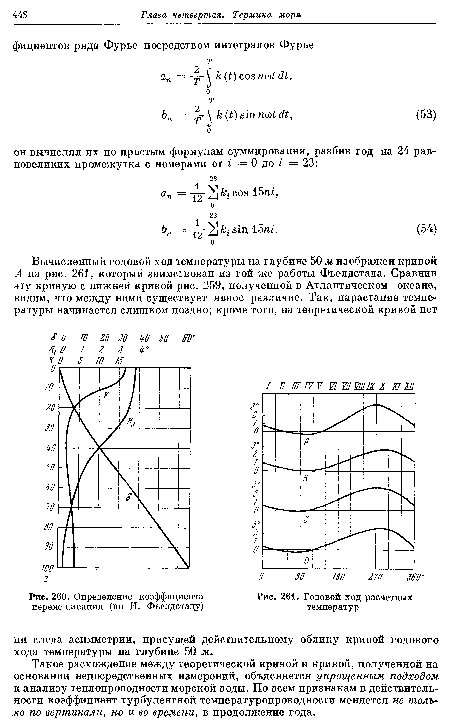 |
| Годовой ход расчетных температур |
 |