Наблюдая волны, движущиеся поблизости от берега, нетрудно обнаружить, что направление их движения здесь не остается постоянным. Даже если в открытом море направление движения волн параллельно берегу, то в пределах материковой отмели они постепенно заворачивают к берегу и подходят к нему иногда почти по направлению нормали.[ ...]
Однако объяснение это чисто качественное. Между тем само явление чрезвычайно интересно как с теоретической (в связи с кинематикой и динамикой волн), так и с практической стороны. Ведь внимательное наблюдение показывает, что волны прибоя подходят к береговой черте далеко не всегда по направлению нормали; весьма часто они идут под довольно значительным углом к нормали.[ ...]
К каким последствиям ведет такой «косой прибой», знает всякий, кому приходилось высаживаться со шлюпки на берег без всяких причальных приспособлений. Но, помимо того, совершенно несомненно, что косой прибой совсем иначе действует на береговые породы, разрушает берег и влияет на портовые сооруя ения по сравнению с прибоем, идущим по нормали к береговой черте.[ ...]
Следовательно, применительно к отмеченным случаям весьма полезно знать наперед, при каких условиях волны будут подходить к берегу в направлении, близком к нормали, или под каким углом должна подходить волна в тех или иных конкретных условиях.[ ...]
В переводе на язык точного анализа это значит, что необходимо: а) найти связь между направлением подхода волн к данной точке и условиями распространения волн в исследуемом районе, а также характеристическими элементами самой волны; б) найти уравнения луча в том смысле, в котором понятие о луче применяется в оптике.[ ...]
В связи с этим уместно будет сейчас напомнить отечественную теорию рефракции морских волн на материковой отмели. Она исходит из интересных исторических изысканий А. Н. Крылова, которому удалось расшифровать метод Ньютона, применявшийся для исследований по астрономической рефракции [49].[ ...]
Значительно сложней выражается скорость с на мелководье формулой (39), в которую входит и глубина моря Н, и длина волн на мелководье Я.[ ...]
Как видим, величины Н/Т2 и с/Т оказываются функциями единственного аргумента — параметра а. Следовательно, мы можем графически получить функциональную зависимость между с/Т и Н/Т2, которая будет совершенно универсальной: она пригодится для исследования волн любого периода Т.[ ...]
Для измерения скорости волн необходимо также пользоваться условной единицей, равной 1 м в секунду, деленному на величину периода.[ ...]
В качестве иллюстрации отметим, что для волн с периодом в 6 сек критической зоной окажется полоса с глубинами 18—25 м, для волн с периодом 10 сек — полоса с глубинами 50—70 м.[ ...]
Рисунки к данной главе:
| Схема рефракции волн |
 |
| Условная скорость волн и пока |
 |
| Лучи на мелководье |
 |
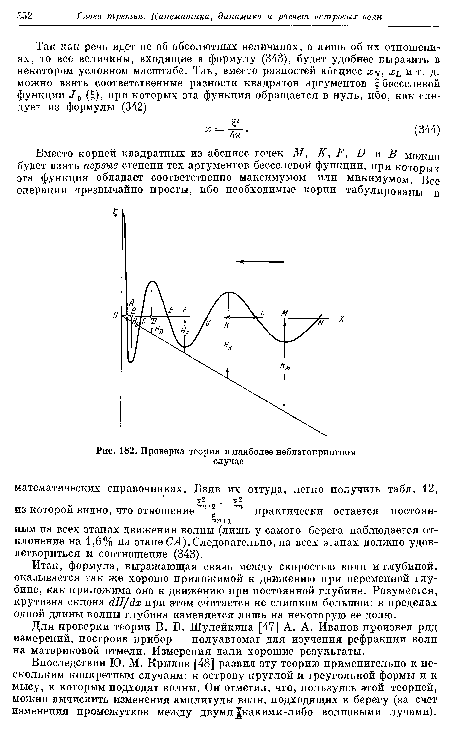
| Проверка теории в наиболее неблагоприятном |
 |