А. П. Хваном на озере Белом, в полном соответствии с теоретическими соображениями В. В. Шулейкинаи его опытами в штормовом бассейне, предельная полувысота установившихся волн на весьма большом расстоянии от наветренного берега пропорциональна не квадрату, а первой степени разности между скоростью ветра и фазовой скоростью волн. Для практических расчетов желательно получить универсальную зависимость по аналогии с той, которая давно утвердилась в аэродинамике для коэффициента лобового сопротивления твердого тела как в турбулентных,так ив ламинарных потоках. Там условно принимают квадратичную зависимость коэффициента сопротивления от скорости потока, или от скорости тела относительно среды, на всем диапазоне скоростей, включая область, где ламинарный поток переходит в турбулентный. В то же время приводят зависимость коэффициента пропорциональности в формулах от числа Рейнольдса.[ ...]
Так и в рассматриваемой задаче надо построить рабочие диаграммы, которые были бы применимы не только к случаю волн в океане или к случаю резко мелководного моря, но и к морям произвольной глубины, характеристики которых являются промежуточными между двумя крайними случаями.[ ...]
На первый взгляд подобная задача может казаться неразрешимой, и она действительно очень долго не поддавалась решению.[ ...]
При вычислениях было принято значение е, найденное из надежных измерений А. П. Хвана на озере Белом: е = 0,02 [42].[ ...]
Следует задаться отдельными значениями а = Н/Я от 0,5 до 3,0 и вычислить соответствующие значения Н Н. Умножив найденные величины Нг/Н на //?, получим значения Н/Нц которые должны отвечать различным значениям И/Н.[ ...]
Здесь коэффициенты К, Ь, М отличаются от принятых в цитированной работе ввиду того, что ряд основных параметров пришлось уточнить в последовавших новых работах.[ ...]
У/УЩ. На рабочей диаграмме рис. 168 также нанесены кривые, которые соответствуют тем же отдельным значениям критерия мелководности, какие фигурируют на рис. 169. На обеих диаграммах эти значения отмечены справа от кривых [43]. Разумеется, при построении принималось во внимание, что правую часть (287) надо делить на 1000, а правую часть (291) — на 3600, если условиться по-прежнему, что х выражается в километрах, а £ — в часах.[ ...]
Анализ новых диаграмм показал, что нет смысла наносить на вспомогательную рабочую диаграмму рис. 167 дополнительные кривые, отвечающие различным значениям критерия мелководности: эти кривые практически совпадали бы с основной, соответствующей океану, при значениях критерия от нуля до единицы. При больших его значениях — на весьма мелководных морях и озерах — кривые отходили бы от основной вдали от начала координат; однако сами различия между ординатами кривых на рис. 168 и 169 при больших значениях абсцисс были бы ничтожно малыми, не представляющими никакого интереса ни с теоретической, ни с практической точки зрения. В заключение сопоставим в табл. 10 вычисленные элементы развивающихся (р) и установившихся (у) волн с полученными по измерениям на морях различной глубины Н1.[ ...]
Рисунки к данной главе:
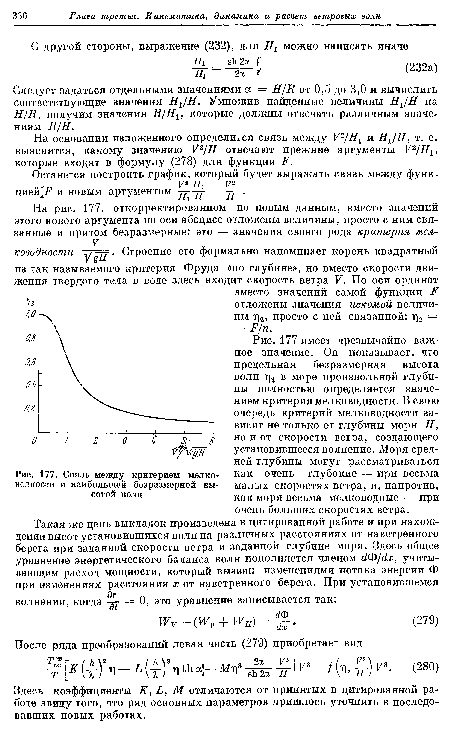
| Связь между критерием мелководности и наибольшей безразмерной высотой волн |
 |