Второй знак равенства поставлен здесь на основании (243). Но применительно к (243) уже было отмечено, что фазовая скорость волн с в точности равна групповой скорости волн при резко выраженном мелководье.[ ...]
Значит, и на резко мелководном море «береговой эффект» продвигается от наветренного берега в открытое море с групповой скоростью — с той скоростью, с какой происходит перенос энергии волнами.[ ...]
Точный интеграл дифференциального уравнения (222), описывающий поле ветровых волн в океане или глубоком море, дает возможность определять безразмерную высоту ц волн, развивающихся за безразмерный срок т действия ветра, или волн, установившихся на безразмерном расстоянии £ от наветренной границы шторма (в частности, от наветренного берега). Для практических расчетов элементов волн необходимо перейти от безразмерных аргументов т, £ к заданным реальным аргументам: времени t, выраженному в часах, и расстоянию х, выраженному в километрах. Что касается искомой высоты волн /г, то она, как помним, просто связана с т); h = r hœ, где hœ — предельная высота волн, которая при заданной скорости ветра V была бы возможна в бесконечно простирающемся океане. Для получения масштабов, необходимых для перехода от безразмерных величин к реальным заданным, начнем именно с масштаба высот волн, их длин и их периодов [37].[ ...]
На рис. 166 по оси абсцисс отложены скорости ветра, выраженные в метрах в секунду, по оси ординат слева — значения hœ в метрах и соответствующие значения предельных периодов волн Tœ, возможных при той же скорости ветра. Справа отмечены значения VTœi которые также будут необходимы в дальнейшем.[ ...]
Парабола hœ построена на основании диаграммы рис. 160 с поправкой на +10%, о которой говорилось выше. Ее ординаты дают значения hœ для заданного значения V: все измеренные наибольшие высоты волн примерно на 10% меньше предельных, которые были бы возможны в безграничном океане.[ ...]
Подставив в (255) предельное значение -—- = 0,82 (см. стр. 311), получим уравнение прямой Тоо, нанесенной на рис. 166. Зная зависимость ТoтF, остается построить вторую параболу F7 oo? позволяющую определить значение этого масштабного отрезка для заданной скорости ветра V.[ ...]
На рабочую диаграмму рис, 167 нанесена кривая Х/Хоо, построенная по этому уравнению, причем Х/Хоо рассматривается как функция rj.[ ...]
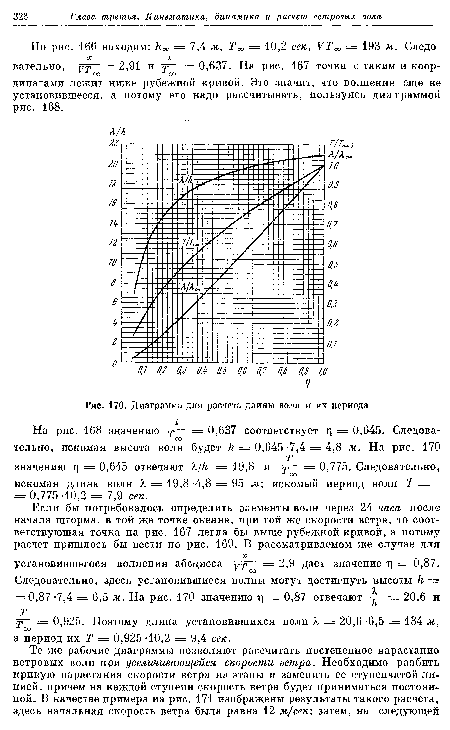
По этой формуле вычислена кривая Я/й, изображенная на рис. 170.[ ...]
Все сомножители под знаком интеграла являются функциями от г . В частности, (Т/Тоо) и (Я/А) снимаются с рабочей диаграммы рис. 170, с одноименных кривых, применительно к последовательно меняющимся значениям г]. Согласно сказанному на стр. 305, положим к = 0,1. Для удобства будем выражать t в часах, a Too — в секундах. Тогда придется в формуле (262) разделить правую часть на 3600.[ ...]
На рабочей диаграмме рис. 168 верхняя кривая вычислена по уравнению (262). Эта кривая относится к условиям океана и очень глубокого моря.[ ...]
Рисунки к данной главе:
| Предельные элементы ветровых волн 5%-ной обеспеченности как функции скорости ветра |
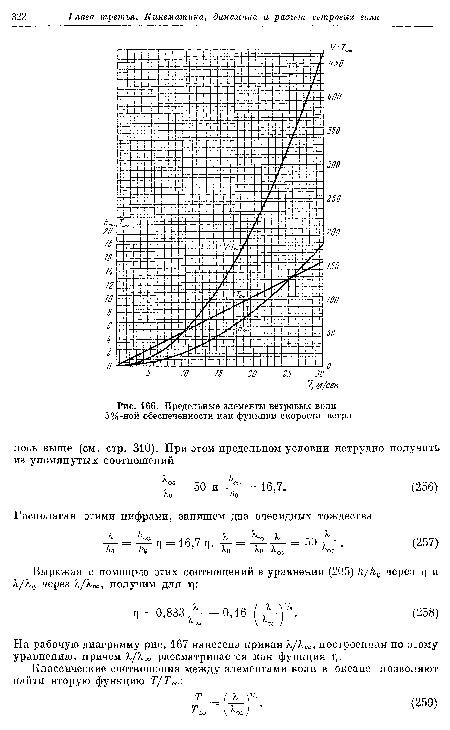 |
| Вспомогательная диаграмма |
 |
| Диаграмма для расчета развивающихся волн |
 |
| Диаграмма для расчета установившихся волн |
 |
| Диаграмма для расчета длины волн и их периода |
 |
| Законы нараста« ния высоты волн при различных режимах ветра |
 |