Если бы ламинарный воздушный поток, проносящийся над гладкой поверхностью воды, не встречал на ней абсолютно никаких неоднородностей — незначительных поднятий и углублений,— зарождение волн было бы немыслимым: абсолютно гладкая поверхность навсегда оставалась бы абсолютно гладкой. Однако в действительности само строение воздушного потока никогда не бывает однородным, в нем всегда существуют хотя бы небольшие завихрения, в связи с которыми давление воздуха на двух близлежащих участках поверхности воды может оказываться не вполне одинаковым.[ ...]
Тем самым обусловлено возникновение мельчайших неоднородностей поверхности воды, лишь кажущейся абсолютно гладкой, а в действительности не являющейся таковой.[ ...]
Независимо друг от друга В. Кельвин [15] и Г. Гельмгольц [16] впервые показали, что при наличии подобных мельчайших возвышений или впадин на гладкой поверхности воды воздушный поток, проносящийся над ней, может вызвать нарастание этих неоднородностей при наличии некоторых определенных условий. Однако условия, необходимые для роста случайных возвышений или впадин на гладкой поверхности воды, на самом деле оказываются совсем не теми, какими они являются в теории Кельвина — Гельмгольца.[ ...]
На это несоответствие указывали последующие авторы, но лишь одному из них — П. Н. Успенскому [17] — удалось найти приближенное истолкование явлений и устранить противоречия в теории зарождения начальных волн. Не останавливаясь на выкладках этого автора, отметим, что он уточнил выражения давления на элементы поверхности воды сверху и снизу. В отличие от задачи, рассмотренной нами в § 2, в задаче о мелких (капиллярных) волнах приходится считаться с наличием разности давлений р±—р2У вызванной поверхностным натяжением; на вершине капиллярной волны вода испытывает давление, превышающее атмосферное, а у подошвы — меньшее, чем атмосферное, именно за счет кривизны натянутого поверхностного слоя.[ ...]
Интеграл, входящий в формулу (143), выражает среднее значение квадрата возвышения элемента поверхности в пределах одной волны. Следовательно, при возрастающей амплитуде колебаний уровня производная от этого интеграла по времени — существенно положительная величина.[ ...]
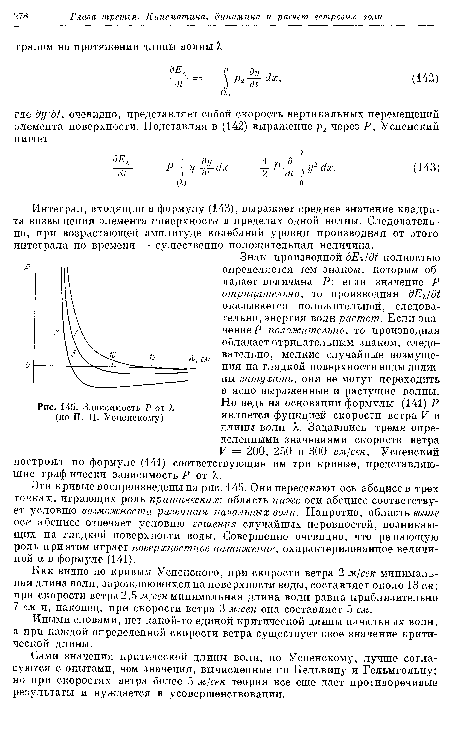
Эти кривые воспроизведены на рис. 145. Они пересекают ось абсцисс в трех точках, играющих роль критических: область ниже оси абсцисс соответствует условию возможности развития начальных волн. Напротив, область выше оси абсцисс отвечает условию гашения случайных неровностей, возникающих на гладкой поверхности воды. Совершенно очевидно, что решающую роль при этом играет поверхностное натяжение, охарактеризованное величиной а в формуле (141).[ ...]
Иными словами, нет какой-то единой критической длины начальных волн, а при каждой определенной скорости ветра существует свое значение критической длины.[ ...]
Сами значения критической длины волн, по Успенскому, лучше согласуются с опытами, чем значения, вычисленные по Кельвину и Гельмгольцу; но при скоростях ветра более 5 м/сек теория все еще дает противоречивые результаты и нуждается в усовершенствовании.[ ...]
Рисунки к данной главе:
| Зависимость Р от X (по П. Н. Успенскому) |
 |