Возникновение пенистых барашков, описанное в предыдущем параграфе, может разрушать вершины волн на сколь угодно глубоком море, лишь бы скорость ветра, создающего дрейфовое течение, была достаточно велика и осредненная скорость возникшего дрейфа превосходила бы предел, установленный формулой (102). Отметим, кстати, что при этом независимо от значения правой части (102) профиль штормовой волны в глубоком море сохраняет симметрию относительно вертикальной оси, проходящей через вершину. Подобный вывод теории, следующий из §§ 9 и 10, подтверждается многочисленными стереофотографиями штормовых волн в океане.[ ...]
Однако существует и иная, чрезвычайно важная причина разрушения волн, нисколько не связанная с ветром и дрейфовым течением. Это — воздействие мелководья на волны (на их профиль).[ ...]
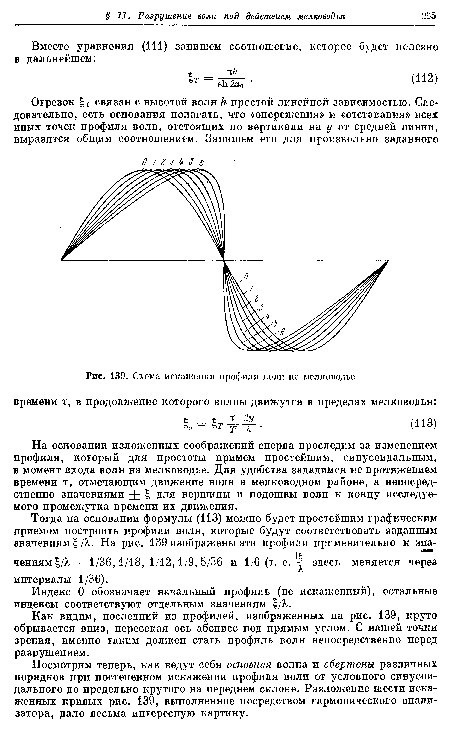
В мелководном море волны никогда не достигают предельной высоты, которая определяется балансом энергии, поступающей от ветра и расходуемой на внутреннее трение в воде. Не успев достигнуть этой высоты, они разрушаются вследствие постепенного и непрерывного искажения их профиля под воздействием мелководья, по которому они распространяются. При этом разрушение гасит несравненно больше энергии, чем тот эффект образования пенистых барашков на гребнях волн, о котором говорилось в § 10. Сейчас мы не будем учитывать этот эффект, а займемся лишь основным явлением, подлежащим исследованию.[ ...]
Влияние мелководья было первоначально исследовано применительно к чрезвычайно длинным (приливным) волнам. Из уравнений гидродинамики было выведено приближенное уравнение профиля приливной волны, первоначально обладавшей простой формой косинусоиды и искаженной под действием мелководья. Был найден приближенный закон нарастания второго гармонического колебания по мере распространения волн в мелководном районе моря.[ ...]
Иными словами, здесь учитывается, что в момент подъема уровня воды на т) выше положения покоя глубина моря становится равной Н + т], а при опускании уровня воды на ц глубина моря уменьшается до значения Н — г .[ ...]
Как известно, в результате нахождения двух последовательных приближений получают форму профиля, искаженную вторым обертоном. При этом не только не предусматриваются появление и постепенное нарастание обертонов более высоких порядков, но даже не учитывается неизбежное уменьшение амплитуды основного колебания в результате передачи все большей и большей части энергии обертонам. Тем самым вводятся весьма грубые ошибки даже в теорию приливных волн, длина которых заведомо очень велика по сравнению с глубиной моря (см. стр. 175).[ ...]
Совершенно незаконными являются рассуждения Г. Джеффриса [12], автоматически распространившего такое грубо приближенное исследование на поверхностные волны и пытавшегося подобным образом выяснить условия разрушения их на мелководье.[ ...]
Здесь X — длина волн, с — их фазовая скорость, — ускорение в поле тяжести, к — высота волн.[ ...]
В результате получается, что даже в очень глубоком море волны должны разрушаться, пробежав расстояние, вытекающее из неверной формулы (105). Действительно, если глубина моря очень велика, то фазовая скорость с от нее не зависит; от глубины моря не зависит и знаменатель правой части формулы (105), содержащий лишь £ и /г. Значит, волны должны разрушаться при любом значении отношения высоты волн к глубине моря.[ ...]
В действительности же волны могут бежать в глубоком море без всякого искажения их профиля неограниченно далеко.[ ...]
Рисунки к данной главе:
| Схема искажения профиля волн на мелководье |
 |
| Нарастание обертонов и понижение основной волны |
 |
| Фотография профиля ветровой волны перед разрушением |
 |