Итак, кинематическое исследование движения частиц на глубинах, существующего при наличии заостренных волн на поверхности моря, позволяет уточнить формальный анализ, который был, в частности, проведен в прежней работе В. В. Шулейкина [1], в результате рассмотрения отдельных обертонов, налагающихся на основную волну.[ ...]
Как видим, теперь не понадобилось применять анализ к системе неразрывно связанных между собой обертонов, которые обязаны обладать общей фазовой скоростью волны. Профиль, зарегистрированный на глубинах, приближается к синусоиде не вследствие «фильтрации» обертонов, а вследствие резкого уменьшения пульсаций стоксова потока на глубинах и быстрого стремления отношения полуосей эллипсов к единице.[ ...]
Одновременно удалось, хотя и приближенно, определить погрешности, которые должны возникать при вычислении размеров орбит на глубинах по формулам, выведенным применительно к трохоидальной, а не заостренной форме волн.[ ...]
В настоящее время появилась возможность исследовать истинную картину [10] исходя из кинематических соображений, приведенных в § 9.[ ...]
Как и в § 9, начнем анализ с простейшего случая волн, распространяющихся при полном безветрии. Прежде всего попытаемся применительно к этим условиям построить траектории поверхностных водных частиц на предельно крутой волне.[ ...]
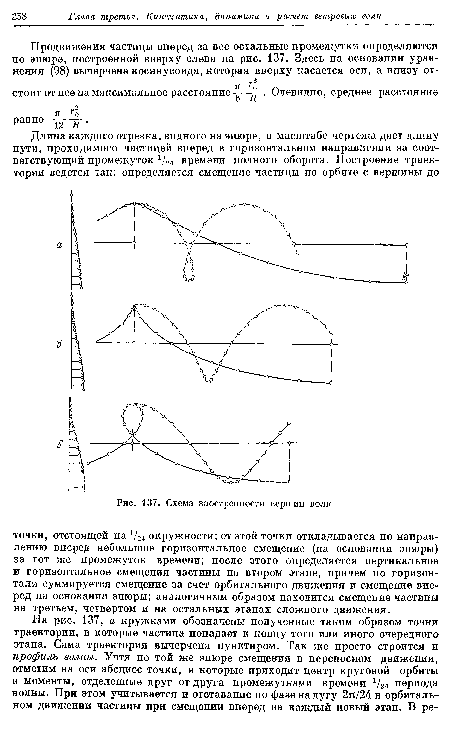
Легко видеть, что профиль, воспроизведенный на рис. 137, а, получился таким же, каким он представлен на рис. 127. Следовательно, два совершенно независимых между собой способа, основанных на современной кинематике волн, привели к результатам, совсем мало отличающимся от выводов точного (формального) анализа.[ ...]
На рис. 137, а профиль по-прежнему характеризуется прямолинейными очертаниями на подходах к вершине, причем угол между прямыми здесь в точности равен 120° в полном соответствии с точной формальной теорией. Неточность получилась у нас лишь у самой вершины, где отсутствует особая (угловая) точка. Следует полагать, что эта неточность была бы устранена, если бы мы пожертвовали компактностью формул, удобством анализа соотношений и учли много членов при разложении в ряд логарифма, выводя формулу (78).[ ...]
Таково кинематическое условие устойчивости волн.[ ...]
Исследуем те выводы, которые вытекают из него в случае распространения ветровых волн. Докажем, что на ветру волны могут разрушаться при меньших значениях h/X и при более тупых углах у вершин.[ ...]
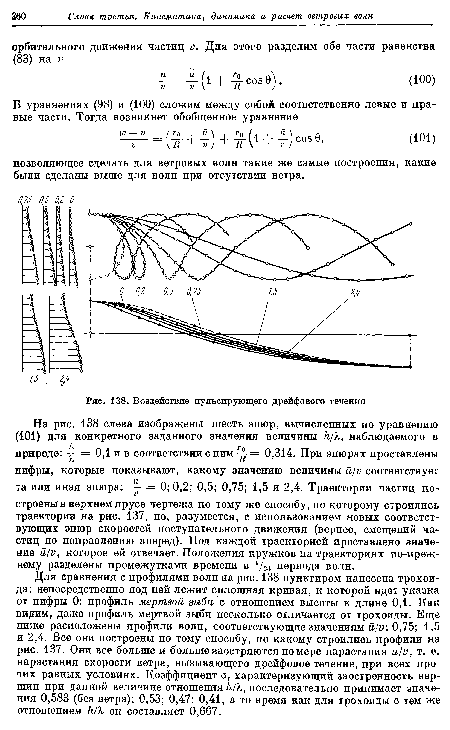
Для сравнения с профилями волн на рис. 138 пунктиром нанесена трохоида; непосредственно под ней лежит сплошная кривая, к которой идет указка от цифры 0: профиль мертвой зыби с отношением высоты к длине 0,1. Как видим, даже профиль мертвой зыби несколько отличается от трохоиды. Еще ниже расположены профили волн, соответствующие значениям й/и: 0,75; 1,5 и 2,4. Все они построены по тому способу, по какому строились профили на рис. 137. Они все больше и больше заостряются по мере нарастания й/и, т. е. нарастания скорости ветра, вызывающего дрейфовое течение, при всех прочих равных условиях. Коэффициент а, характеризующий заостренность вершин при данной величине отношения к/Х, последовательно принимает значения 0,583 (без ветра); 0,53; 0,47; 0,41, в то время как для трохоиды с тем же отношением к/Х он составляет 0,667.[ ...]
Рисунки к данной главе:
| Схема заостренности вершин волн |
 |
| Воздействие пульсирующего дрейфового течения |
 |