Для изучения кинематики двумерных волн, как ветровых, так и мертвой зыби, оказался весьма удобным тот метод, который был предложен В. В. Шу-лейкиным в основном для исследований динамики волн (см. далее). В Морском гидрофизическом институте Академии наук СССР был построен большой кольцевой бассейн, в котором волны могут бегать по окружности как угодно долго под воздействием ветра со скоростью до 19 м/сек и затухают в продолжение определенного времени после прекращения ветра. Один сектор этого штормового бассейна застеклен в обеих стенах, благодаря чему создана возможность кино- и фотосъемок зарождающихся, развивающихся, установившихся и затухающих волн. Железная арматура стекол одновременно служит координатной сеткой.[ ...]
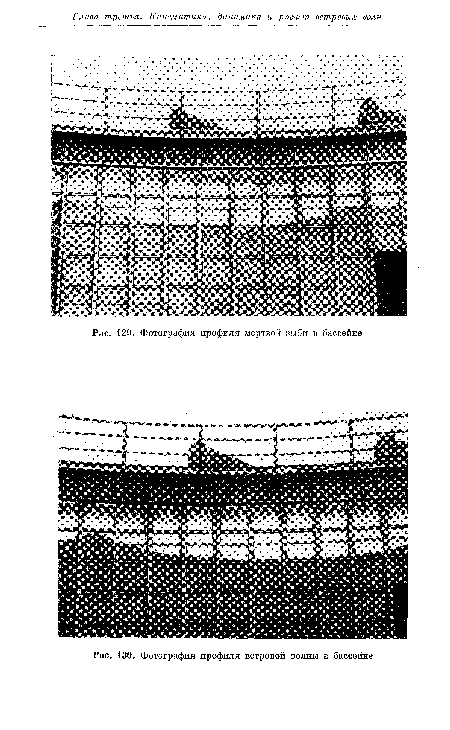
На рис. 129 воспроизведена фотография мертвой зыби, полученной в бас сейне. Здесь профиль приблизительно трохоидальный (хотя, как увидим ниже, даже и в случае подобной зыби он все же отличается от трохоиды).[ ...]
На рис. 130 приведена фотография ветровой волны в том же бассейне. У нее уже нет ничего общего с трохоидой: при вершине видна угловая точка, как у «максимально крутой» безветровой волны (рис. 127), формально изучавшейся гидродинамиками, но угол при вершине здесь более тупой.[ ...]
При современных исследованиях [7, 8] удалось найти общие уравнения семейства кривых, к которому принадлежат наблюдаемые профили ветровых волн и к которому в качестве частного вида принадлежат трохоиды.[ ...]
Пусть высота ветровой волны равна / =2Ь, а ее длина X. Направим ось X координатной системы вдоль прямой, проходящей через середины высот волн в направлении движения волн. Ось У направим вертикально вверх. Волны будем считать двумерными (плоская задача).[ ...]
По уравнениям (69) легко построить профиль ветровой волны, если заданы параметры а и Ь: можно вычертить эллипс с полуосями а и 6, разметить на нем точки, соответствующие различным значениям 0, перемещать центр эллипса вдоль оси X на отрезки, равные Д0, и отмечать на неподвижном листе бумаги соответствующие положения точки, движущейся по эллипсу. Легко убедиться в том, что при правильном выборе значений параметров а и Ь полученная кривая изобразит типичный профиль ветровой волны, соответствующий этим значениям параметров.[ ...]
На рис. 131 изображен один из профилей, полученных посредством киносъемки в штормовом бассейне.[ ...]
Вершины волн здесь отсекают на оси X отрезки АВ, которые значительно короче отрезков ВС, отсекаемых подошвами волн.[ ...]
На рис. 127 нанесена сплошная кривая, построенная по уравнениям (69), при таких значениях параметров. Небольшие расхождения с пунктирной кривой заметны только у самой вершины волны.[ ...]
Это соотношение позволяет судить о степени заострения волн, профиль которых принадлежит к исследуемому семейству. В частности, при п = 1 выражение (72) дает значение о для трохоиды. В пределе, при N — 0, а обращается в единицу, как и следовало ожидать в случае синусоидальных волн, у которых к бесконечно мало по сравнению с Я.[ ...]
Рисунки к данной главе:
| Фотоаппаратура штормового бассейна |
 |
| Фотография профиля ветровой волны в бассейне |
 |
| Характеристика заостренности вершин волн |
 |
| Подводный фонарик |
 |