Как известно, это — уравнения трохоиды, записанные в параметрической форме.[ ...]
Круг радиусом R называется кругом качения, окружность радиусом г„ — производящей окружностью.[ ...]
Если г() очень мало по сравнению с i?, то вычерченная трохоида весьма близка по форме к синусоиде с той же длиной волн А, и с той же их высотой = 2г0.[ ...]
Чем больше значение r0/i?, тем явственнее сказывается различие между трохоидальным и синусоидальным профилями, — тем острее становятся вершины волн и тем положе их подошвы.[ ...]
К количественному сопоставлению различных профилей волн мы вернемся в § 8 настоящей главы.[ ...]
В предыдущем параграфе было показано, что круговращательное движение частиц, заданное уравнениями (3), в чрезвычайно глубоком море обязано затухать по экспоненциальному закону при удалении вниз на все большие и большие расстояния Ъ. Это вытекает из условия неразрывности, т. е. уравнения (2). Посмотрим теперь, как должно на подобного рода движениях сказаться влияние дна, находящегося не так глубоко под поверхностью моря.[ ...]
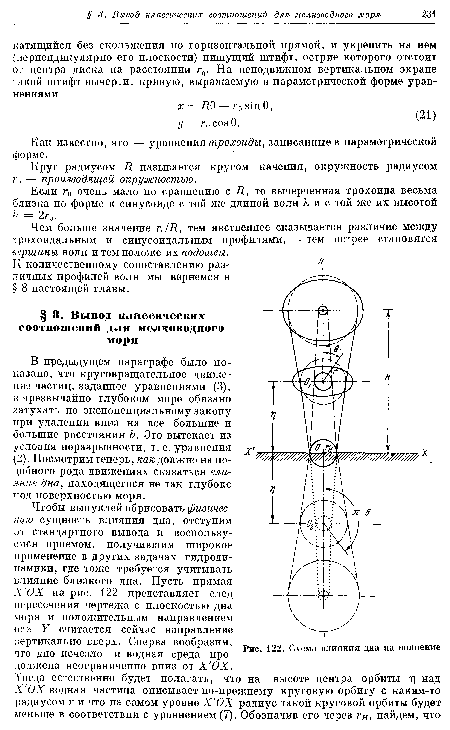
Чтобы выпуклей обрисовать физическую сущность влияния дна, отступим от стандартного вывода и воспользуемся приемом, получившим широкое применение в других задачах гидродинамики, где тоже требуется учитывать влияние близкого дна. Пусть прямая Х ОХ на рис. 122 представляет след пересечения чертежа с плоскостью дна моря и положительным направлением оси Y считается сейчас направление вертикально вверх. Сперва вообразим, что дно исчезло и водная среда продолжена неограниченно вниз от Х ОХ.[ ...]
В многочисленных задачах гидродинамики принято учитывать влияние дна, рассматривая как бы зеркальное изображение тела, движущегося в водной среде, причем зеркалом служит плоскость дна. Найдя такое зеркальное изображение, можно удалить дно и рассматривать движение исследуемого тела совместно с движением его «двойника» в безграничной водной среде.[ ...]
Попытаемся последовать этому примеру и нанесем на рис. 122 зеркальное изображение частицы, движущейся по окружности вокруг центра Ог. Получим двойник, который должен описывать такую же орбиту радиусом г, но только против часовой стрелки вокруг точки 02, которая находится на расстоянии т] ниже координатной оси ОХ.[ ...]
Легко заметить, что в исследуемый момент времени радиус-вектор, проведенный из 02 в зеркальное изображение движущейся точки, составит угол л — 0 с положительным направлением оси Y.[ ...]
Рисунки к данной главе:
| Схема влияния дна на волнение |
 |
| Зависимость эллиптичности орбит от глубины моря |
 |