Недавние катастрофические наводнения, порожденные подводными зем летрясениями на Тихом океане, вызвали к жизни целую серию новых исследований по этой проблеме как теоретических, так и экспериментальных, — и в нашей стране, и в Японии, особо подверженной вторжениям волн цунами.[ ...]
На путях к решению этой чрезвычайно сложной общей задачи Л. Н. Сретенский совместно с А. С. Ставровским дал в окончательном виде решение упрощенной задачи о высотах волн цунами в различных точках береговой черты (без учета влияния кориолисовой силы) [20].[ ...]
Ось X направлена вдоль берега, считающегося прямолинейным в исследуемом районе; ось У перпендикулярна берегу и направлена в океан. Интеграл уравнения (148) записан в [20] применительно к произвольно заданному закону изменения /. Простейшее решение получается, если /(я, у, т) = Кг, причем К — постоянная величина, отличная от нуля только на протяжении отрезка, параллельного оси X, с концами, отстоящими от оси У на расстояния + I. Этот отрезок удален от оси X на расстояние у о. Во всем остальном пространстве К = 0.[ ...]
Область £> определяется пересечением этого конуса с полоской в той же системе координат, определяемой условиями: — I < х I; 0<т< Т; у = 0.[ ...]
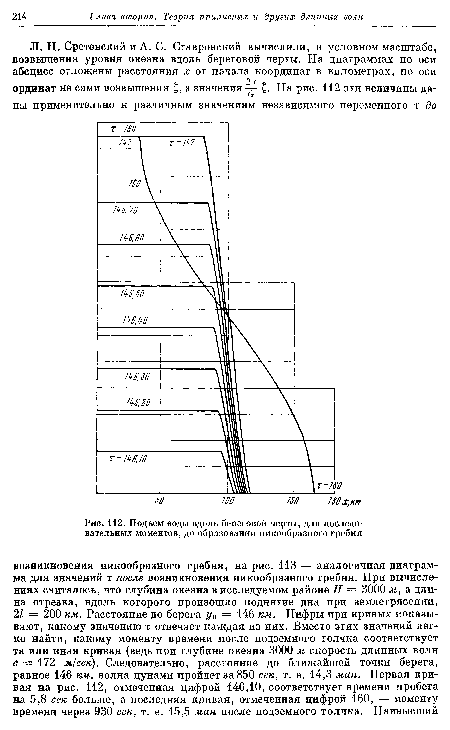
Очень интересна диаграмма Л. Н. Сретенского и А. С. Ставровского, представленная на рис. 114. Она по-иному освещает исследованное ими явление: показывает, по какому закону изменяется во времени уровень океана в различных пунктах побережья. Расстояния каждого из этих пунктов от начала координат записаны при каждой кривой. По оси абсцисс вместо времени отмечены в оригинале значения независимого переменного т, связанного с £ прежним соотношением. Добавлены отметки времени, отсчитываемого в минутах, с момента подводного толчка. Из диаграммы видно, что в точках побережья, удаленных от начала координат не более чем на 100 км, уровень океана стремительно подымается до пика, а затем монотонно падает; в точках побережья, лежащих далее 100 км от начала координат, подъем происходит все более и более плавно, приближаясь к максимальному уровню, а после него уровень все медленней и медленней падает.[ ...]
Авторы произвели вычисление также и для второго варианта: вместо 21 — 200 км задались протяжением отрезка, на котором происходит подъем дна, 21 — 10 км. Применительно к такому условию возвышение уровня океана над положением покоя, вдоль береговой черты, меняется так, как показано на рис. 115. Над пиками отмечены соответствующие значения независимого переменного т, а близ максимальных ординат проставлены их значения в прежнем условном масштабе.[ ...]
Определение этого условного масштаба и переход от цифр, проставленных на осях ординат всех трех диаграмм, станет возможным тогда, когда сейсмологи найдут закон изменения скоростей / подъема дна во время подводных землетрясений и позволят наилучшим образом аппроксимировать гипотетическое соотношение (151).[ ...]
Уравнение третьего порядка в частных производных (142), возникшее при учете изменений глубины Н океана, должно привести, в конечном счете, к несравненно более сложному уравнению в обыкновенных производных, чем уравнение четвертого порядка (144). Совсем непреодолимые затруднения возникали бы при попытках аналитического решения задач применительно к волнам цунами в проливах, где меняется не только глубина Н, но и расстояние между берегами.[ ...]
Между тем именно в проливах увеличивается опасность волн цунами и возрастает потребность в детальном изучении возможных наибольших высот этих волн. В частности, это относится ко Второму Курильскому проливу, берега которого нередко подвергаются опасности. Вот почему большой практический интерес представляет моделирование длинных волн применительно к условиям этого пролива.[ ...]
Естественными границами на модели служили берега. Одна из искусственных границ была параллельна фронту волны, создаваемой при быстром опускании бруса-волногона. Две другие границы были перпендикулярны этому фронту — они осуществлялись волногасительными приспособлениями. На некотором протяжении, до входа в пролив, глубина бассейна была постоянная: воду можно было наполнять до высоты слоя около 29 см (в одной серии было принято Н = 28,9 см, в другой — 29,5 см). Датчики, служившие для регистрации колебаний уровня воды в проливе, были основаны на принципе изменения сопротивления в электрической цепи. В каждом датчике было по два серебряных цилиндрических электрода, отделенных друг от друга водой бассейна. При колебаниях уровня колебалась длина столба воды между электродами. Одновременно работали девять таких датчиков, включенных в цепь шлейфов двух осциллографов МПО-2. Вся система работала на переменном токе с напряжением 4,5 в и частотой 50 гц. Запись на пленках осциллографов получалась в виде широких волнообразных полос. На тех же лентах осциллографов автоматически отмечались моменты времени. За начало отсчета условно принимался момент прохождения волны через датчик № 1. Температура воды была постоянной во всех точках бассейна : 19,4°.[ ...]
Рисунки к данной главе:
| Подъем воды вдоль береговой черты, для последовательных моментов, до образования пикообразного гребня |
 |
| Изолинии относительных возвышений. Волна с юга |
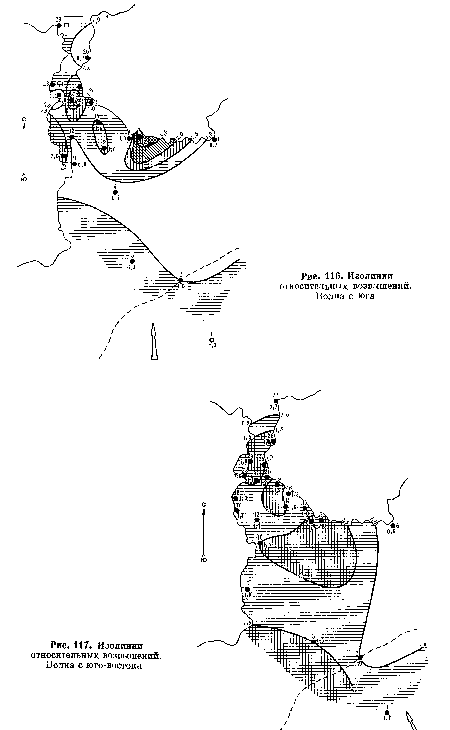 |
| Изолинии относительных возвышений. Волна с юго-востока |
 |
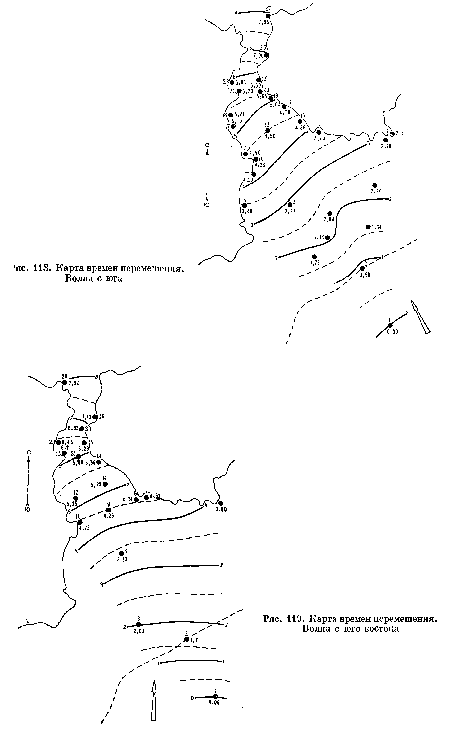
| Карта времен перемещения. Волна с юго-востока |
 |