Только что произведенный анализ показывает, что даже при простом очертании берегов замкнутого моря и при постоянной его глубине закон свободных колебаний в нем выражается сложной функцией. Совершенно очевидно, что в реальных природных условиях явление еще больше осложняется благодаря особенностям рельефа дна и очертаний берегов.[ ...]
Однако существуют способы исследования собственных колебаний вод в таком сложно очерченном море, позволяющие находить достаточное приближение к истинной картине даже в случае весьма сложной конфигурации морского ложа.[ ...]
Рассмотрим здесь исследования в этом направлении, принадлежащие Д. Кристэлу [8]. Его метод заключается в следующем.[ ...]
Прежде всего трехмерная задача приводится к двумерной: определяется профиль дна некоторого эквивалентного моря, обладающего более простой формой, но теми же самыми гидродинамическими характеристиками. Ширина такого эквивалентного моря выбирается постоянной, очертания его принимаются прямоугольными, а глубина изменяется только в продольном направлении, в поперечном же глубина для каждого сечения сохраняется неизменной.[ ...]
Для нахождения профиля дна этого эквивалентного моря оказывается достаточным проделать весьма простую операцию: в направлении наибольшей протяженности в море выбирают некоторую стрежневую линию и разбивают ее на достаточно большое число участков. Во всех нанесенных точках строят поперечные сечения моря и вычисляют их площади 5Л., которые затем умножают каждую на соответствующую ширину сечения Ък (считая по поверхности моря).[ ...]
Полученная кривая представляет собой профиль дна эквивалентного моря; в плане это море, как было уже сказано, имеет прямоугольную форму. Но далеко не для всякого профиля дна задача о свободных колебаниях вод еще может быть разрешена. Ее удалось разрешить только для нескольких типичных форм, очертание которых укладывается в простые аналитические соотношения. Во всех остальных случаях приходится определять, к какой из этих типовых форм ближе всего подходит профиль того или иного эквивалентного моря.[ ...]
При других профилях, изображенных на рис. 97, таких простых соотношений между периодами ТУ ТУ Т3, ... не будет, так как узловые линии расположатся совсем иначе. Индексы 1, 2, 3. ... теперь будут обозначать только число возникающих углов, а не кратность. Сам период одноузловой сейши также зависит от формы профиля дна, как это показывает первый столбец прилагаемой табл. 7; период Т0, соответствующий постоянной глубине, принят за единицу. В остальных столбцах приведены отношения периодов многоузловых сейш к периоду одноузловой — для всех типов профиля, изображенных на рис. 97.[ ...]
На более сложных профилях не останавливаемся.[ ...]
Недостатком метода Кристэла является его сложность. К тому же он позволяет определять только периоды многоузловых сейшен, но не дает указаний о расположении самих узлов и пучностей. В этом отношении от него выгодно отличается другой метод, предложенный А. Дефантом [9] и основанный на последовательных приближениях.[ ...]
Здесь величины £0 и т]0 играют роль переменных амплитуд, зависящих только от координаты х исследуемой точки. Они должны, очевидно, удовлетворять условиям (13) и (106), т. е.[ ...]
Рисунки к данной главе:
| Схемы различных профилей дна |
 |
| Схема профиля поверхности моря |
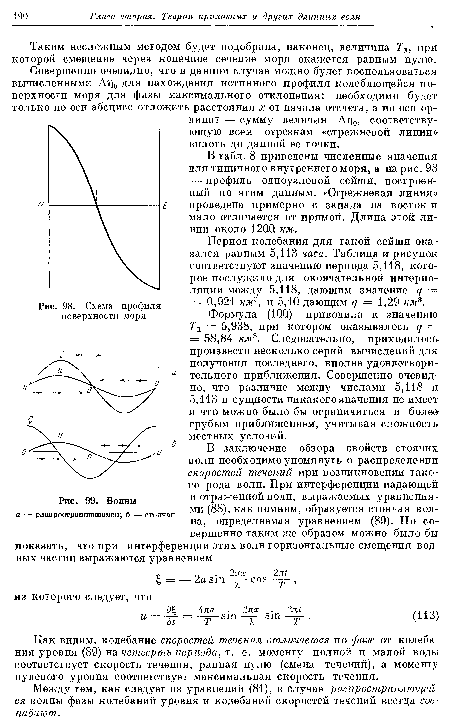 |
| Волны а — распространяющаяся; б - |
 |