На всем протяжении выкладок, заимствованных из оригинальных работ Экмана и других исследователей, развивавших его теорию, пока предполагалось, что водная среда моря однородна по температуре, солености и, следовательно, по плотности. В таких условиях легко определялась глубина, на которой практически обращается в нуль скорость дрейфового течения — это так называемая глубина трения Д, на которой скорость течения составляет 11ек = 0,043 от скорости поверхностного дрейфа. Между тем исследования течений в океане и на глубоких морях показывают, что нередко на весьма больших глубинах существуют течения с довольно большими скоростями. Ояп порождены перестройкой поля плотностей, происходящей главным образом благодаря возникновению дрейфовых течений в верхних слоях, при неоднородной среде вод моря или океана. Одним из первых исследователей подобных сложных явлений был П. С. Линейкин, показавший, что весьма важные результаты можно получить, анализируя течения в неоднородной среде при учете диффузии плотности.[ ...]
Здесь [хх и —соответственно коэффициенты горизонтального и вертикального турбулентного обмена количеством движения, причем считается возможным отождествить их с соответствующими коэффициентами плотностной диффузии в тех же направлениях.[ ...]
Рассматриваются течения, возбуждаемые ветром в бесконечно глубоком канале, ограниченном с боков отвесными параллельными стенками. Считается, что в начальный момент поверхность воды горизонтальна, течения отсутствуют, плотность воды линейно возрастает по вертикальной оси, направленной вниз (оси X). Ось У совпадает с направлением стенок и ветра, дующего вдоль канала. Следовательно, искомые проекции скорости гг, и,и>, давление воды р, плотность ее 6 и понижение уровня £ не должны зависеть от у.[ ...]
Условие (331) основано на допущении, что ни ветер, ни течения не меняют теплового режима на поверхности моря.[ ...]
Все переменные величины, входящие в уравнения, заменяются безразмерными переменными путем внесения некоторых масштабных значений. Например, вместо координаты х рассматривается безразмерная координата х = х!Ь, причем/, — ширина канала. Остальные масштабы построены как комбинации 1Х, 12, £, и других заданных параметров.[ ...]
После этого сложная система уравнений (323) — (327) приводится к линейной системе из четырех уравнений в частных производных второго и первого порядков. Начальные и граничные условия выводятся из уравнений (328) — (331), путем упомянутой замены переменных.[ ...]
Напомним, что Ъ, зависящее от градиента плотности по вертикали, выражено третьей слева формулой в (329).[ ...]
При заданных параметрах оказалось /) = 45 м, Н = 1000 м, т. е. толщина бароклинного слоя примерно в 22 раза больше, чем глубина трения по Эк-ману.[ ...]
Из рис. 68 видно, что отрезок между точкой О на кривой б и точкой О на кривой а составляет примерно г/3 от вектора, проведенного из начала координат в точку О на кривой а. Следовательно, добавочное векторное слагаемое, обусловленное градиентно-конвекционным течением, здесь достигает 1/3 от экмановского чисто дрейфового вектора. За счет этого слагаемого модуль полной скорости на поверхности моря возрастает на 12,5%. Эта поверхностная скорость составляет с направлением ветра угол 32° вместо 45° — величины, характеризующей направление чисто дрейфового течения.[ ...]
Рисунки к данной главе:
| Изогипсы на вращающейся модели при переменном / |
 |
| Часть карты изобат нулевой поверхности (по ¿4. Дефанту) |
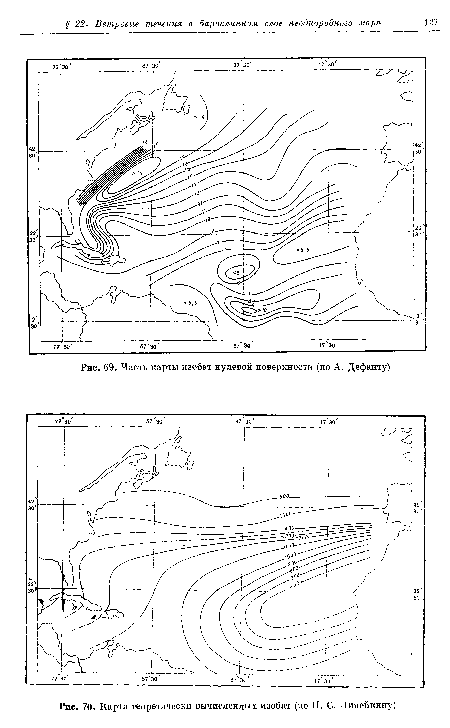 |
| Карта теоретически вычисленных изобат (по П. С. Линейкину) |
 |
| Теоретические линии тока в Атлантике (по А. С. Саркисяну) |
 |