Чисто дрейфовые течения, теория которых была изложена в § 8, могуг иметь место только в открытом океане, вдали от берегов. Вблизи же береговой черты, как было уже упомянуто в предыдущем параграфе, всякий дрейфа неминуемо приводит либо к понижению, либо к повышению уровня цоря, вызывая сгоны или нагоны вод [6].[ ...]
К сожалению, до настоящего времени еще никому не удалось дать полное решение задачи применительно к граничным условиям, представляющим наибольший практический интерес: к условиям наклонного дна, постепенна понижающегося по мере удаления от берега. При этих условиях приходится обязательно учитывать вертикальные составляющие скоростей течения, иными словами, приходится иметь дело со всеми тремя уравнениями из системы типа (42). До настоящего времени полное решение задачи давалось лишь для случая отвесной береговой стенки при постоянной глубине моря до самого берега и для особого случая, описанного в § 13.[ ...]
Рассмотрим режим прибрежной зоны, предполагая, что береговая линия — прямая, протянувшаяся безгранично в обе стороны. Допустим сперва, что ветер направлен под каким угодно углом р к береговой линии, на так, что берег находится вправо от него. Такой ветер, очевидно, должен вызвать дрейфовый поток, одна из составляющих которого будет направлена к берегу (см. стр. 31), а потому он является нагонным.[ ...]
Но нагон поверхностных вод ведет к повышению уровня моря по направлению к берегу, другими словами, к возникновению градиента давления. Со своей стороны создавшийся градиент вызывает градиентное течение, которое в главной толще воды направляется, очевидно, перпендикулярно к градиенту, а стало быть, вдоль берега и притом вправо, если смотреть с берега на море.[ ...]
Оставив пока в стороне это преобладающее «глубинное» течение, вспомним о течении «придонном». Оно, как следует из (63) и из рис. 12, обладает составляющими скоростей, перпендикулярными к береговой линии.[ ...]
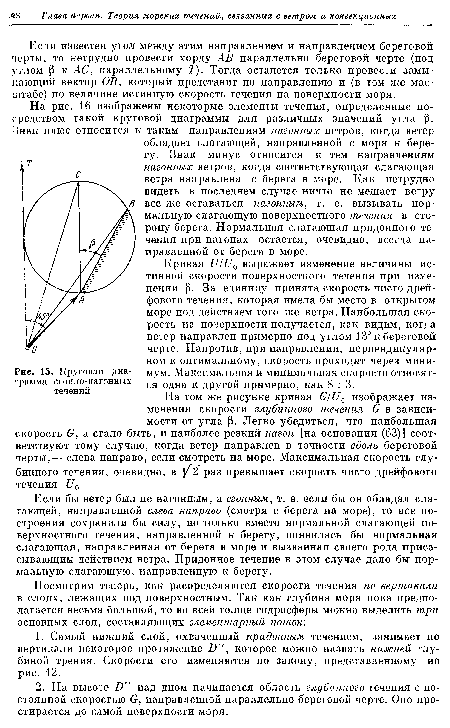
Воспользовавшись этим соотношением, определим сперва величину и направление поверхностного течения, предполагая, что берег чрезвычайно приглубый, а потому глубину моря до самой отвесной стенки берега можно считать бесконечно большой. В таком случае можно построить весьма простую векторную диаграмму, которая позволит находить искомые течения для каких угодно направлений ветра.[ ...]
Это соотношение весьма замечательно. Прежде всего оно устанавливает связь между поверхностной скоростью, которая имела бы место в случае чистого дрейфа, и скоростью реально существующего глубинного течения. Затем на основании этого уравнения оказывается возможным построить векторную диаграмму, о которой идет речь.[ ...]
Совершенно очевидно, что действительная скорость на самой поверхности моря должна представлять собой геометрическую сумму двух векторов: а) скорости градиентного течения G, простирающегося до самой поверхности моря, и б) скорости «дрейфа», вызываемого ветром (U0).[ ...]
Следовательно, для определения величины и направления скорости на поверхности моря, при всевозможных направлениях ветра, практически следует поступать так. Надо построить вектор ОА, представляющий по направлению и по величине (в некотором заданном масштабе) скорость чисто дрейфового течения, которая, как увидим в дальнейшем, может быть весьма просто вычислена на основании эмпирических соотношений по известной скорости ветра. Затем следует построить окружность на отрезке АС = ОЛУ 2, как на диаметре: она коснется оси Г, совпадающей с направлением ветра.[ ...]
Рисунки к данной главе:
| Круговая диаграмма сгонно-нагонных течений |
 |
| Схема элементарного потока |
 |
| Диаграммы (в плане) для различных направлений ветра |
 |