На основании этих соотношений вычислены годографы скоростей на различных горизонтах, воспроизведенные на рис. 12. Три кривые отвечают случаям, когда глубина моря равна соответственно 0,25 D, 0,5 D и 1,25 D. Как видим, в мелководном море течение на всех горизонтах мало отклоняется от направления градиента, но уже при глубине моря 0,5 D отклонение в поверхностных слоях значительно превышает 45°.[ ...]
В тех случаях, когда глубина моря превышает глубину трения D, распределение скоростей происходит по закону, имеющему громадное значение, как увидим в дальнейшем. Именно вся толща морской воды, лежащая над дном выше, чем D, движется в одном и том же направлении■—перпендикулярно к градиенту. Только в слое высотой D, лежащем непосредственно над дном, скорости течения меняются по величине и направлению в зависимости от расстояния от самого дна. Высоту D, следовательно, можно назвать «нижней глубиной трения».[ ...]
Легко видеть, что она играет здесь роль, совершенно аналогичную «верхней глубине трения» в дрейфовом течении. Ведь можно вообразить, что дно моря движется относительно гидросферы, и трение между дном и придонным слоем воды играет ту же роль, что и тангенциальная сила Т при дрейфе. Вот почему скорость течения в слое, непосредственно прилегающем ко дну, отклонена на угол 45° от действующей силы.[ ...]
В действительности трение сильно осложняет развитие градиентного течения, но нетрудно видеть, какого рода изменений следует ожидать в только что рассмотренных движениях водных частиц. Прежде всего скорость поступательного движения частиц иг при наличии трения будет вести себя примерно так, как вела себя скорость развивающегося дрейфового течения [см. уравнения (58) и рис. 11]. Только «затухание» колебаний вектора здесь пойдет значительно быстрей, и скорость иг через непродолжительное время приобретет установившиеся величину и направление.[ ...]
Что касается вращательного движения частиц, то составляющие нестационарного режима и2 и v2 не исчезнут очень долго.[ ...]
Среди градиентных течений особое место занимает важная их разновидность — конвекционные течения, возникающие благодаря различию плотностей морской воды на одной и той же глубине. Подобное различие создает неравенство давлений на одной и той же глубине, создает соответствующий градиент давлений. О таких течениях нам приходилось уже говорить в предыдущих параграфах настоящей главы: их элементы мы определяли, пользуясь динамическим методом анализа гидрологических разрезов и применяя к ним теорему о циркуляции (см. § 6 и 7).[ ...]
Там при выводе соотношения (39) пришлось пренебречь силами трения, и оставалось неясным, насколько законно ими пренебрегать. Здесь будет уместно вернуться к этому важному вопросу, вооружившись новым методом исследования, позволяющим детально проследить за распределением скоростей течения по вертикали.[ ...]
Первая попытка такого исследования, принадлежащая Экману, повела к недоразумению, распространившемуся весьма широко и остававшемуся необнаруженным десятки лет. Оно было обнаружено В. Б. Штокманом в 1949 г. [81.[ ...]
Изложим здесь его выводы, позволяющие по-новому смотреть на строение конвекционных течений.[ ...]
Перенесем начало коодинат на нижнюю границу слоя, охваченного конвекционным течением, и направим ось Z вверх. Тогда условия (66) будут соответствовать, в новом обозначении, г = 0, а значению г = Нг будут соответствовать условия на поверхности моря.[ ...]
Рисунки к данной главе:
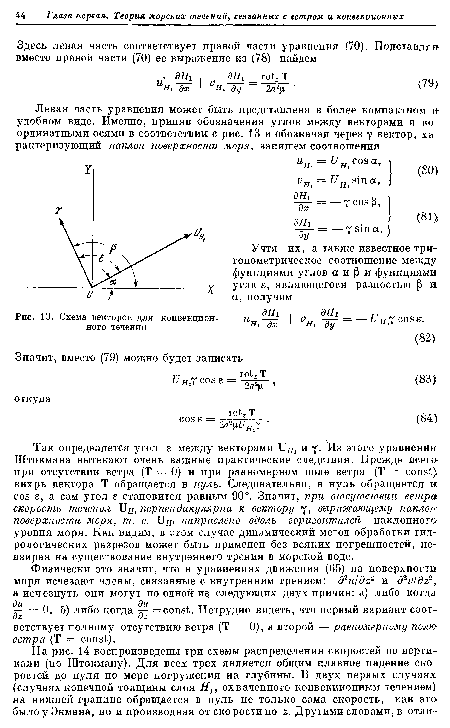
| Схема векторов для конвекционного течения |
 |
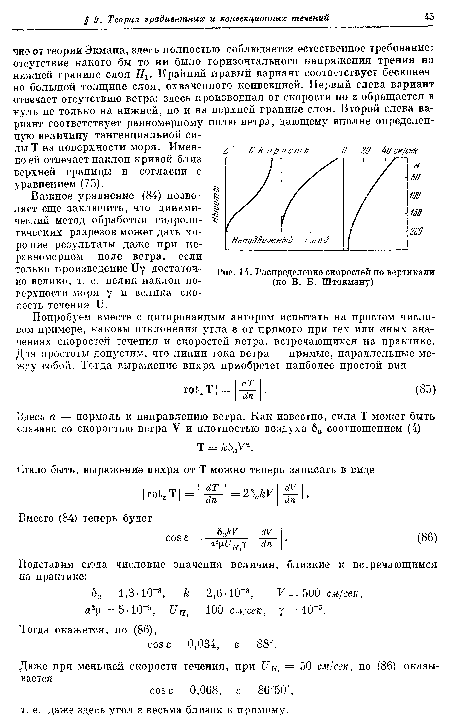
| Распределение скоростей по вертикали (по В. Б. Штокману) |
 |