В общих чертах об этом было уже упомянуто на стр. 12. Теперь же на основании формулы (39) оказывается возможным получить величину скорости течения по такой динамической карте.[ ...]
Чем чаще расположены на карте динамические горизонтали, тем больше, очевидно, будет скорость течения.[ ...]
Что касается направления скоростей, то они должны совпадать с касательными к горизонталям в любой их точке, если только на частицы воды не действуют никакие иные силы, кроме силы тяжести и силы Кориолиса. В дальнейшем будет показано, в каких случаях подобное допущение законно и в каких оно не соответствует действительности.[ ...]
Динамический метод обработки гидрологических элементов получил в настоящее время широкое распространение.[ ...]
В предыдущем параграфе изложены методы определения скорости установившегося течения, применяемые в современной океанографии и основанные на теории циркуляции. Как было уже упомянуто, точная трактовка вопроса сопряжена с весьма большими трудностями ввиду неопределенности члена Я, входящего в формулу (34) (см. § 6). Вот почему все вычисления предыдущего параграфа исходят из упрощенного допущения, что трение отсутствует, а потому 7? = 0. Однако подобное допущение не всегда законно. Оно привело бы к неверным результатам, если бы мы стали исследовать процесс развития течения хотя бы под воздействием ветра («дрейфового» течения). Даже в случае установившегося течения оно дало бы превратное представление о распределении скоростей по вертикали, если бы мы захотели проследить за изменением вектора скорости по глубине в поверхностном слое дрейфового течения, поддерживаемого исключительно ветром.[ ...]
Такое же неправильное суждение составилось бы и по отношению к придонному течению в море ограниченной глубины независимо от того, вызывается ли это течение неоднородностями водной среды (различием плотностей) или разностью уровней поверхности моря, появившейся хотя бы под влиянием нагона или сгона вод у береговой черты.[ ...]
Нечего и говорить о том, что различные нестационарные задачи заставляют считаться с наличием внутреннего трения в водных массах. Словом, внутреннее трение в море играет решающую роль в большинстве современных задач физики моря, так или иначе связанных с течениями.[ ...]
В настоящее время четко наметились два рода таких задач, идейно связанных между собой, поскольку они преследуют общую цель (исследование потоков в море), но формально решаемых различными путями.[ ...]
Подобные условия (условия преобладания сил трения первого рода) действительно соблюдаются в ряде случаев: там, где сильно выражен турбу-лентный обмен между горизонтальными слоями на всех глубинах, там, где потоки проходят в мелководных областях моря, обеспечивая перемешивание водных масс до самого дна, и т. п. Однако в очень большом числе случаев эти условия не соблюдаются, заставляя тем самым сомневаться в справедливости первой схемы. Не соблюдаются эти условия в сильно неоднородном (по плотности) море с большими глубинами; в переслоенной водной среде, с большим градиентом плотностей по вертикали, слабо развивается турбулентный обмен между горизонтальными слоями, а потому коэффициент трения между ними оказывается весьма малым.[ ...]
Здесь вступают на сцену задачи второго рода, сравнительно недавно» привлекшие к себе внимание исследователей. При решении их учитывают силы трения на вертикальных границах между водными массами, исходя из экспериментально определенных величин соответствующего коэффициента трения которые в 106 и даже в 107 раз превышают значения коэффициентов трения х между горизонтальными слоями вод. Считаясь с таким большим различием в порядках коэффициентов рь и рл, пренебрегают трением потоков о дно океана, ибо без подобного упрощения не удалось бы решить задачи второго рода современными математическими методами.[ ...]
Рисунки к данной главе:
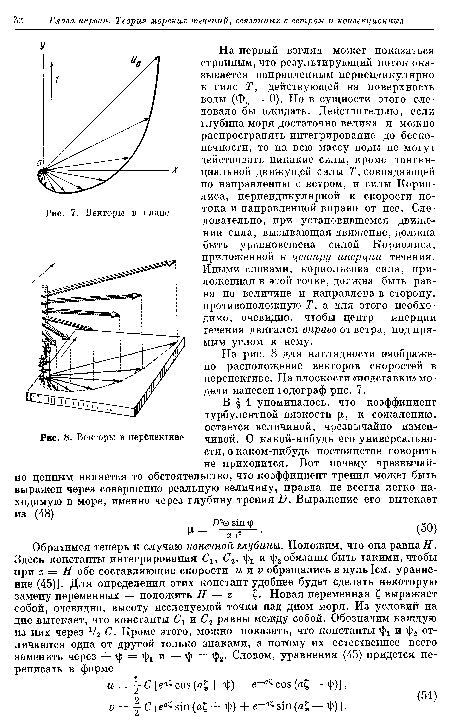
| Векторы в плане |
 |
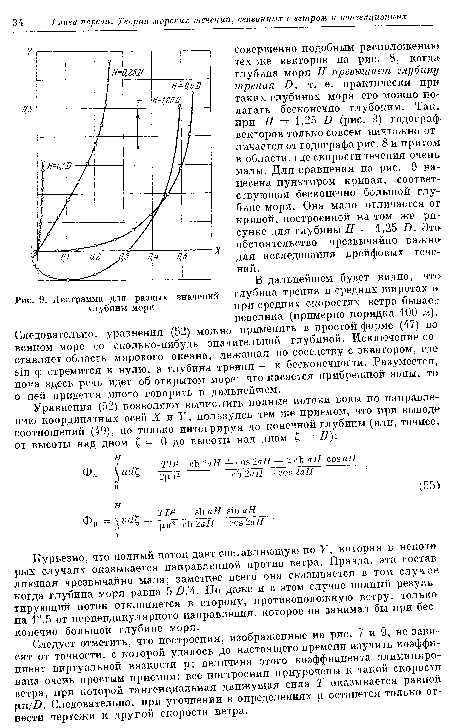
| Векторы в перспективе |
 |
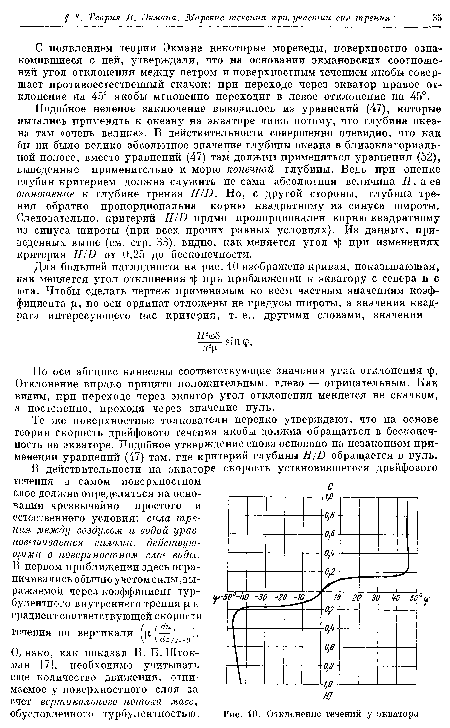
| Диаграмма для разных значений |
 |
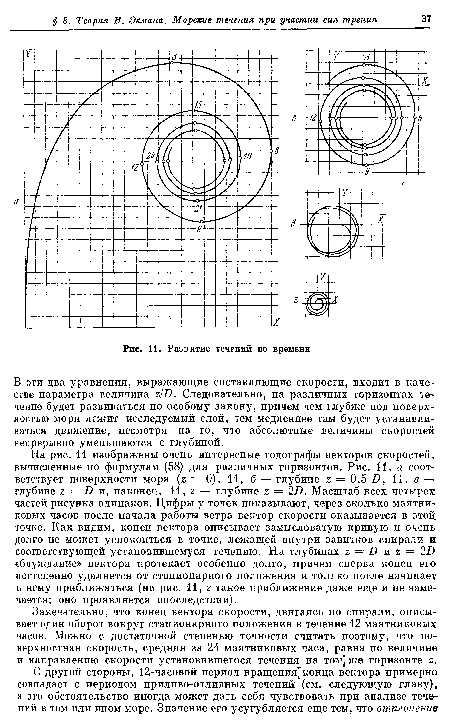
| Отклонение течений у экватора |
 |
| Развитие течений во времени |
 |