Способы, посредством которых контролируется численность популяции вида, — наиболее важный аспект ее ниши. Механизмы контроля и некоторые другие аспекты ниши не являются в действительности ресурсами сообщества. Примем, однако, допущение, что имеется некоторое соответствие между тремя признаками: частью гиперпространства ниши сообщества, которую занимает вид, частью ресурсов сообщества (свет, вода, пища и т. д.), которую вид использует, и частью продукции сообщества, которую вид производит. Будет понятнее для нашей задачи, если мы оставим в стороне признаки ниши, не относяшиеся к категории ресурсов, и таким образом упростим п-мерное пространство ниши до т-мерного пространства ресурсов. Мы вправе тогда спросить, каким образом это пр странство ресурсов делится между видами и какие типы относительной значимости видов являются результатом такого разделения.[ ...]
Предложен ряд гипотез для толкования этих кривых. Когда они были сформулированы, казалось возможным трактовать их как варианты рабочей гипотезы и использовать наблюдения над реальными соотношениями значимости видов в сообществе для выбора наиболее приемлемого из них.[ ...]
Здесь N — сумма значимостей всех видов в описании; гц — вначнмость вида 1 в последовательности от наиболее значимого к наименее значимому виду, с — отношение значимости каждого вида к каждому предшествующему ему виду в последовательности, гм — значимость первого и наиболее важного вида.[ ...]
Здесь вг — число видов в октаве, удаленной иа Л октав от модального интервала, который содержит в0 видов; а — постояниаи, которая часто приближается к 0,2.[ ...]
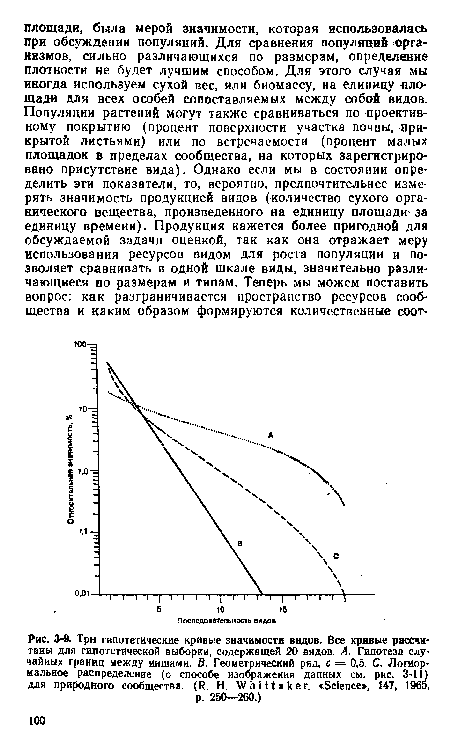
На рис. 3-9 одновременно показаны три формы кривых распределения значимости видов для гипотетических сообществ. Теперь уже получено немало выборок данных для природных сообществ, которые могут быть сопоставлены с с этими кривыми. Эмпирические результаты не совпадают полностью ни с одной из трех выдвинутых гипотез. Рис. 3-11 иллюстрирует некоторые реальные описания: (Л) небольшой учет популяций гнездящихся птиц, статистика которого приближается к кривой случайных границ между нишами; (В) высокогорный пйхтовый лес в горах Грейт-Смоки-Маунтинс, с распределением видов, близким к геометрическому ряду; (С) богатый видами лес в ущелье в тех же горах, аппроксимируемый логнормальным распределением. Различные описания сообществ показывают соответствие всем трем моделям и переходам между ними. Вместо формального выбора одной из трех моделей для нас важнее выяснить, в каких случаях и почему кривые значимости видов в сообществе соответствуют каждой из этих кривых.[ ...]
Мы заключаем, что: 1) общее представление — разграничение пространства ресурсов (и ниши) сопровождается ослаблением конкуренции между видами — может лежать в основе существования различных по форме кривых значимости видов, но 2) разнообразие форм этих кривых, ранжированных от геометрической через логнормальную к кривой случайных границ, проявляется лишь тогда, когда значимость анализируется у разных групп организмов и разных сообществ; в этих случаях 3) учеты, если они включают ограниченное число видов, связанных друг с другом конкуренцией в пределах одного и того же сообщества, могут соответствовать кривой случайных границ ниш или геометрической форме, тогда как 4) для учетов, которые включают большое число видов, независимо от того, являются ли они конкурентами или нет и получены ли они из одного или нескольких сообществ, соответствующей будет логнормальная форма.[ ...]
Рисунки к данной главе:
Вернуться к оглавлению