В гл. I мы рассмотрели пример популяции, в которой возникает еще одно нетривиальное равновесие (популяция с нижним критическим порогом численности или популяции типа Олли). Вообще ’’эффект Олли”, т.е. увеличение скорости роста популяции при объединении отдельных особей во взаимодействующие группы (самым простым примером такого объединения служит возникновение репродуктивных пар) может приводить к возникновению нескольких нетривиальных положений равновесия. Переход популяции из одного состояния в другое может происходить как вследствие естественной эволюции системы, так и под действием случайных возмущений. Иногда с такими переходами связывают понятие ’’эластичности” сообщества. Точнее, система считается ’’эластичной”, если случайные воздействия не разрушают ее, а приводят в другое стационарное состояние. Среди равновесных точек системы могут встречаться как устойчивые, в окрестности которых система будет проводить большую часть времени, так и неустойчивые, которые связаны с границами областей притяжения устойчивых состояний.[ ...]
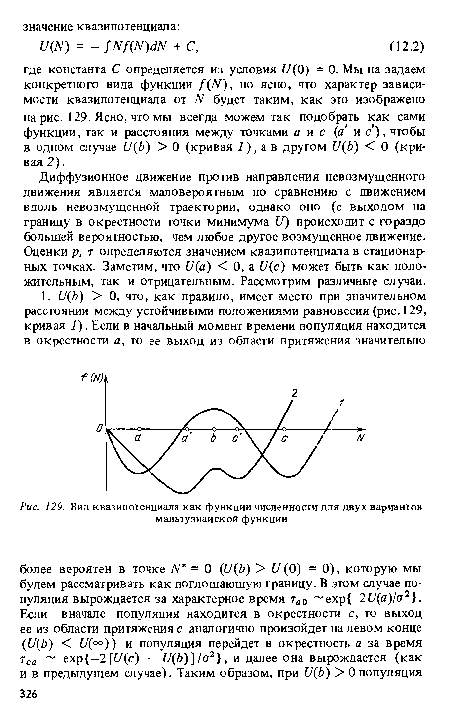
Диффузионное движение против направления невозмущенного движения является маловероятным по сравнению с движением вдоль невозмущенной траектории, однако оно (с выходом на границу в окрестности точки минимума II) происходит с гораздо большей вероятностью, чем любое другое возмущенное движение. Оценки р, т определяются значением квазипотенциала в стационарных точках. Заметим, что 1/(а) < 0, а и (с) может быть как положительным, так и отрицательным. Рассмотрим различные случаи.[ ...]
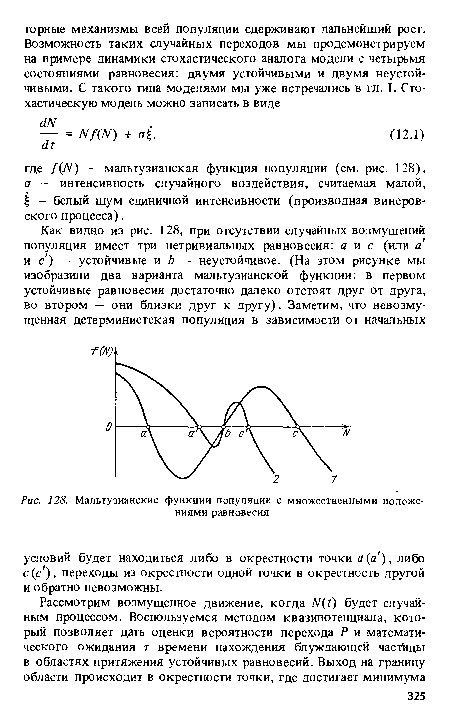
Переходя к экологической интерпретации полученных результатов, напомним, что рассматривается модель популяции с четырьмя стационарными состояниями, два из которых устойчивы. Обратимся вновь к рис. 128. Если устойчивые положения равновесия а и с разделены большим диапазоном численности (а < Ь, кривая 1). то система вырождается за характерное время т ехр —2U(a)/o2 . В этом случае популяция сильно отличается от логистической, интервал положительного прироста популяции при малых численностях достаточно мал по сравнению с интервалом, где при средних численностях начинают сказываться механизмы, угнетающие рост популяции (и даже делающие его отрицательным). Это могут быть механизмы конкуренции, которые никак не компенсируются, например, механизмами коллективной адаптации, включающимися при более высоких значениях численности. В результате популяция просто не успевает дойти до этих численностей и вырождается под действием случайных возмущений.[ ...]
Рисунки к данной главе:
| Мальтузианские функции популяции с множественными положениями равновесия |
 |
| Вид квазипотенциала как функции численности для двух вариантов мальтузианской функции |
 |