Кроме классификации границ к качественным моделям изучения случайных процессов следует отнести исследование таких свойств, которые проявляются на всей области определения и характерны для процесса в целом на больших интервалах времени. К этим свойствам, в первую очередь относятся возвратность по отношению к той или иной области, наличие стационарного распределения и условия устойчивости равновесного решения соответствующего динамического уравнения.[ ...]
Рассмотрим условия возвратности процесса, определяемого уравнением (10.1). Как уже указывалось, это явление имеет место для интервала регулярности процесса N(t) (a(N) Ф 0; N € (г!, г2)) при отталкивающих границах. Таким образом, из классификации границ следует, что свойство возвратности характерно лишь для случайных процессов, порождаемых флуктуациями коэффициента конкуренции, а при флуктуациях а — лишь при а <е, т.е. при достаточно низкой их интенсивности. Тогда логистические популяции, возмущаемые белым шумом, не вырождаются и не достигают больших размеров, однако значительные колебания численности в пределах значений (г , г2) вполне вероятны.[ ...]
Константа С определяется из условия /р0 (N) dN= 1.[ ...]
В заключение отметим, что если обсуждаемые уравнения динамики популяций понимать в смысле Стратоновича, то картина приведенных результатов качественного анализа получается аналогичной, с той разницей, что в случае возмущений мальтузианского параметра границей перехода от притяжения к отталкиванию в нуле является условие а2а < 2а0 (а не <а0) и соответственно меняется условие существования стационарного распределения. Это означает, что если структура случайных возмущений удовлетворяет схеме Стратоновича, то условия на допустимую интенсивность (например, с точки зрения вырождения) являются более слабыми.[ ...]
Рисунки к данной главе:
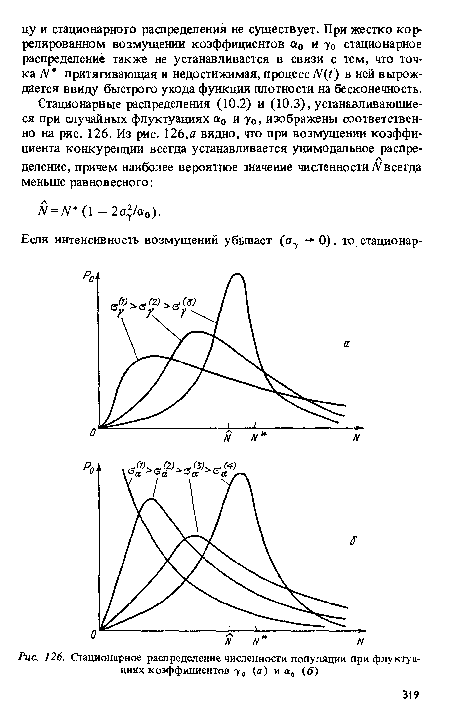
| Стационарное распределение численности популяции при флуктуациях коэффициентов у„ (а) и«, (б) |
 |