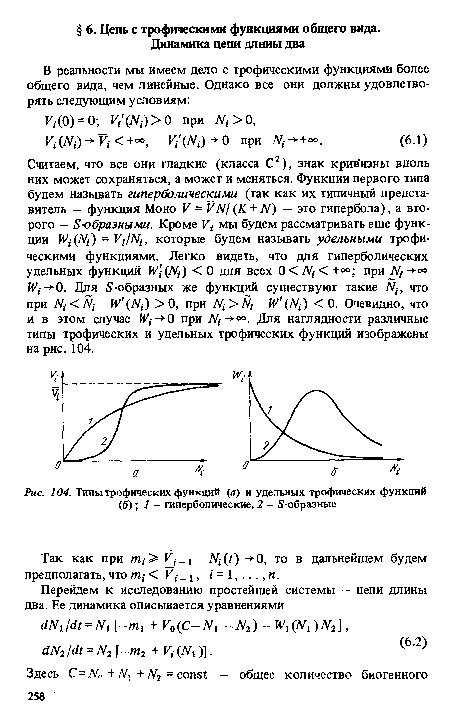
Для 5-образных же функций существуют такие N¡, что при N¡<Ñj W (N¡) >0, при Nt>Ñi W (N¡) <0. Очевидно, что и в этом случае W¡- 0 при N - °°. Для наглядности различные типы трофических и удельных трофических функций изображены на рис. 104.[ ...]
Так как при т,> К, t Nt(t) ->0, то в дальнейшем будем предполагать, что ш,- < V j, i = 1,..., п.[ ...]
Переходя к анализу устойчивости этих точек, мы получим, что при С>С2 первые две точки являются седлами, и из внутрь положительного квадранта выходит сепаратриса.[ ...]
Выше (§ 2) была доказана ограниченность траекторий замкнутой трофической цепи. Поэтому, применяя теорему Дюлака— Бендиксона, мы получаем следующий результат.[ ...]
В случае W (N ) < 0 существует такоеСкр >С2, что при С >Скр система (6.2) имеет устойчивый предельный цикл.[ ...]
Заметим, что при W (С2- Ct) < 0 обычным для системы (6.2) является рождение предельного цикла в результате бифуркации Андронова—Хопфа, так как с ростом параметра С фокус N теряет устойчивость. Очевидно, что бифуркационное значение С р есть корень уравнения R (С£р) = 0, и, как показано выше, хотя бы один такой корень всегда существует.[ ...]
Для ответа на вопрос об устойчивости рождающихся циклов нужно вычислить первую ляпуновскую величину. Процедура эта довольно стандартная, хотя и громоздкая, а получающееся в результате выражение совершенно необозримо. Поэтому прошу мне поверить, что соответствующие выкладки мной сделаны и показано, что ляпуновская величина может принимать разные знаки. Отсюда сразу следует, что в системе (6.2) возможен как мягкий, так и жесткий режим возбуждения автоколебаний.[ ...]
Заметим еще, что если в результате бифуркации рождается неустойчивый предельный цикл, то он всегда будет окружен устойчивым циклом.[ ...]
Рисунки к данной главе:
| Типы трофических функций (а) и удельных трофических функций (б); 1 - гиперболические, 2 - 5-образные |
 |