Второе многообразие зависит только от одного параметра Хк — ’’емкости” среды для популяции жертв. На рис. 97 в плоскости (X, У) изображены два вида этой кривой при различных значениях .[ ...]
Здесь можно говорить, что в точках У = С1<2 отображение Ж(У) прямой на прямую имеет особенность. Эта особенность является складкой и представляет собой простейший тип катастрофы. Но, согласно теореме Уитни, эта особенность устойчива, т.е. она не исчезает при малых шевелениях самого отображения. Устойчивость такого типа называется еше структурной.[ ...]
Рисунки к данной главе:
| Равновесное многообразие У = F(X) для системы (5.1); 1 - Хк < <ч/27; 2-Хк>^П |
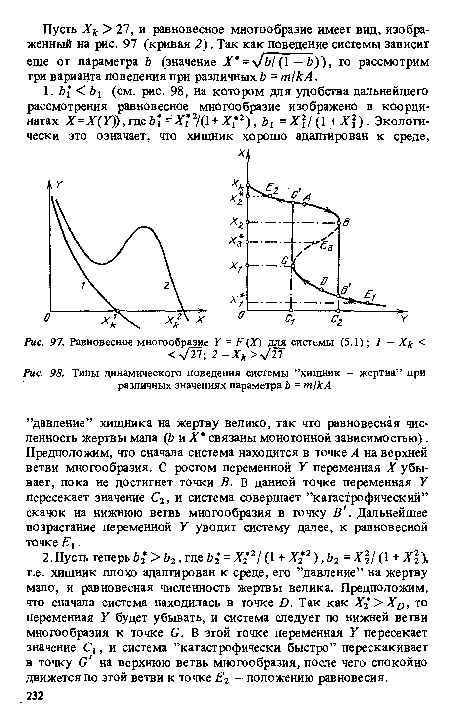 |
| Типы динамического поведения системы ’’хищник - жертва” при различных значениях параметра Ъ = т/к А |
 |