Система для определения временной части решения - вольтер-ровская. Ее интеграл известен, и решение представляет собой периодические колебания (с периодом J mJa в малом) вокруг равновесия (Л , Я ).[ ...]
Уравнения для пространственной части решения описывают гармонические колебания с периодом а относительно того же равновесия.[ ...]
Здесь А — введенный ранее линейный оператор, имеет собственные пространственные функции cos - ™х в соответствии с выбранными условиями непроницаемости границ.[ ...]
Таким образом, векторные уравнения (7.4) - (7.6) образуют замкнутую систему обыкновенных дифференциальных уравнений, которые и отражают динамику исходной системы (7.1) вблизи точки бифуркации.[ ...]
Таким образом, в подкритической области начало координат — узел, в надкритической области — седло, следовательно, происходит перестройка фазового портрета в окрестности однородного равновесия, представленная на рис. 90. Здесь до и после бифуркации существует лишь одно равновесие, переходящее из узла в седло.[ ...]
Рисунки к данной главе:
| Область устойчивости однородного решения системы (6.2) (АехАт < <0) |
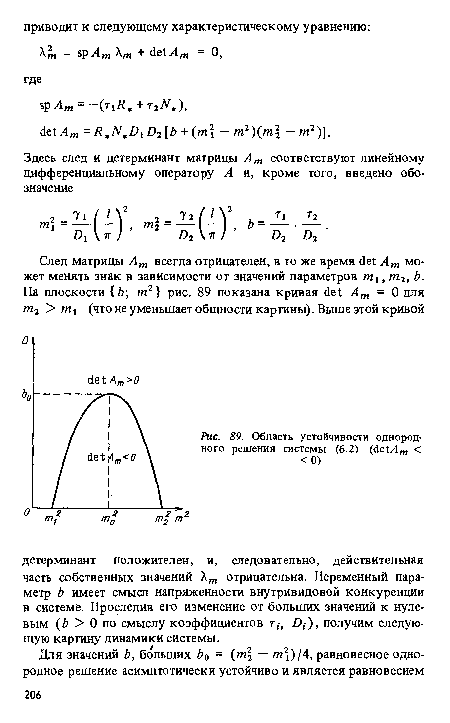 |
| Перестройка фазового портрета в окрестности равновесия в момент бифуркации |
 |
| Области параметров, определяющих существование неоднородных решений нелинейной задачи |
 |