Любопытные примеры популяционных волн дает нам теория эпидемий. Рассмотрим некоторую популяцию, в которой распространяется безыммунная эпидемия. Считается, что заражение особей происходит при непосредственном контакте больных и здоровых (основным примером здесь служит распространение венерических заболеваний, в частности, гонореи), а их перемещения в пространстве носят чисто случайный характер и подвижности больных и здоровых одинаковы; смертность отсутствует. Тогда локальная модель эпидемии может быть описана следующим образом.[ ...]
Здесь Р — доля больных, выявляемых органами здравоохранения за единицу времени, а — ’’частота контактов” в расчете на особь. Заметим, что, например, по данным США а = 2,1 контактов в неделю.[ ...]
Если /3 < -, то первое из них неустойчиво, а второе устойчиво.[ ...]
Приведем простой пример. Предположим, что около 30% заболевших в течение месяца обращается к врачу, массовых обследований не производится и контакты заболевших не выявляются. Тогда (р = 66,7 миль за месяц) а = 8,5, /3 = 0,3 и v — 166 миль за месяц. Расстояние в 3000 миль эта эпидемия пройдет за полтора года.[ ...]
Другой случай порогового эффекта по плотности появляется, если считать, что частота контактов зависит от общей плотности популяции, т.е. а = а(М).[ ...]
Очевидно, что должно быть выполнено ограничение gc < /3.[ ...]
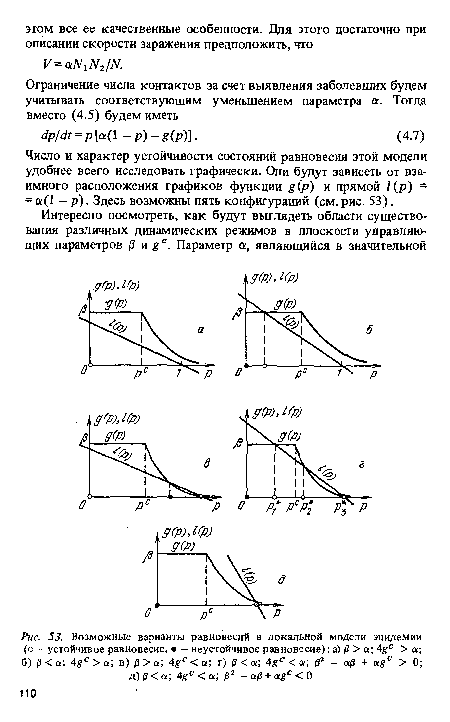
Число и характер устойчивости состояний равновесия этой модели удобнее всего исследовать графически. Они будут зависеть от взаимного расположения графиков функции g(p) и прямой I(р) = = а(1 - р). Здесь возможны пять конфигураций (см. рис. 53).[ ...]
Очевидно, что если 0 и g° (т.е. доля обследуемых и доля обслуживаемых) достаточно велики, то эпидемии не возникнет (область 1, соответствующая случаю, изображенному на рис.53,а). Наиболее интересен с динамической точки зрения 4-й режим, соответствующий рис. 53, г, в котором могут существовать четыре состояния равновесия: два устойчивых и два неустойчивых. В пространственном варианте любая локальная вспышка в этом режиме будет порождать сложную волновую картину.[ ...]
При этих начальных условиях (4.9) имеет решение типа бегущей волны. Другими словами, при начальных условиях типа локальной эпидемии по ареалу будет распространяться волна эпидемии со скоростью v = oNy/2a.[ ...]
Рисунки к данной главе:
| Возможные варианты равновесий в локальной модели эпидемии (о - устойчивое равновесие, • - неустойчивое равновесие) |
 |
| Области существования различных динамических режимов в плоскости (0, gc) при а = 0,8 |
 |