В промежутках между вспышками почкоед малочислен, хотя совсем не исчезает, сохраняясь в некоторых локальных очагах. В этом состоянии его численность контролируется насекомоядными птицами и паразитами. Однако этот контроль не очень эффективен, и всегда существует порог численности, превосходя который, почкоед ’’ускользает” из-под этого контроля.[ ...]
Вспышка не может возникнуть до тех пор, пока трофический ресурс (лес) не восстановится после предшествующей вспышки. Вспышка обычно развивается в зрелом лесе или лесе промежуточной зрелости. Следовательно, промежуток между вспышками должен составлять от 30 до 100 лет. Конечно, это, если можно так выразиться, необходимое условие для возникновения вспышки. Кроме этого, возникновение вспышки существенно зависит от погодных условий (сухое, жаркое лето).[ ...]
В среднем вспышка продолжается от 7 до 16 лет, причем она охватывает территории площадью до 105км2, а линейные размеры распространения достигают от нескольких сотен до тысячи километров (восток Канады, провинция Нью-Браунсвик).[ ...]
Как и многие другие виды насекомых, почкоед обладает очень большой миграционной способностью. Средняя квадратичная величина расселения за поколение составляет около 50 км. Регистрировались перемещения и в несколько сотен километров, однако эти перемещения были связаны с большими циклонами и существенно не влияли на общую картину распространения вспышки, приводя лишь к возникновению малых локальных очагов, достаточно далеко удаленных от основного очага, генерирующего главную волну распространения почкоеда. Поэтому в дальнейших расчетах мы примем величину р = 50 км за год.[ ...]
Наиболее тщательно была изучена вспышка 50—60-х годов, по этим данным Холлинг построил для своей модели зависимости мальтузианской функции г от плотности популяции, выраженной в числе личинок на м2 площади ветвей для трех типов леса: молодого леса, леса промежуточной зрелости и зрелого леса (см. рис. 49). Поскольку эта вспышка распространялась в основном по зрелому лесу, то из результатов Холдинга мы получаем, что г = 2,4 год-1. Другая оценка получается, если использовать данные Морриса по плодовитости елового почкоеда и по факторам смертности.[ ...]
Для определения доверительного интервала использовалась i-статистика с 10%-ным уровнем значимости. В одну выборку объединялись значения г (0), полученные за два последовательных года на 10 контрольных деревьях. Любопытно, что для последней вспышки три оценки мальтузианского параметра, сделанные различными способами, дали близкие значения.[ ...]
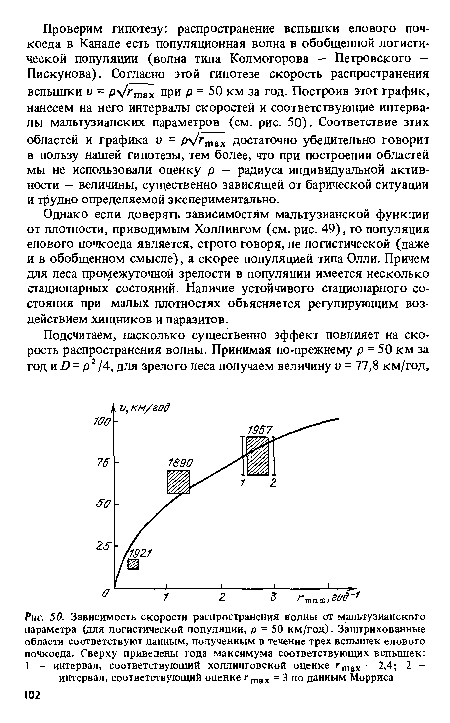
К сожалению, в нашем распоряжении не было карт распространения вспышек, а была лишь информация типа: ”на следующий год значительная степень поражения наблюдалась в районах, расположенных в 60-70 км к югу” (для вспышки 1890 г.). Аналогичный интервал для скорости (10—20 км К юго-западу) отмечался для вспышки 1921 г. Поэтому говорить здесь о какой-либо статистике бессмысленно - можно указать лишь интервал оценки.[ ...]
Известно, что по последней вспышке существует более подробная информация о географическом распространении елового почкоеда (особенно по провинции Нью-Браунсвик). Однако и в этом случае мы имели лишь экспертную оценку 80 + 10 км/год (личное сообщение проф. Т. Хатчинсона из Торонтского университета).[ ...]
Однако если доверять зависимостям мальтузианской функции от плотности, приводимым Холдингом (см. рис. 49), то популяция елового почкоеда является, строго говоря, не логистической (даже и в обобщенном смысле), а скорее популяцией типаОлли. Причем для леса промежуточной зрелости в популяции имеется несколько стационарных состояний. Наличие устойчивого стационарного состояния при малых плотностях объясняется регулирующим воздействием хищников и паразитов.[ ...]
Рисунки к данной главе:
| Гистограмма распределения скоростей распространения вспышки (---- возможный вид аппроксимирующего распределения) |
 |